题目内容
【题目】为了解本届高二学生对文理科的选择与性别是否有关，现随机从高二的全体学生中抽取了若干名学生，据统计，男生35人，理科生40人，理科男生30人，文科女生15人。
(1)完成如下2×2列联表，判断是否有99.9%的把握认为本届高二学生“对文理科的选择与性别有关”？
男生 | 女生 | 合计 | |
文科 | |||
理科 | |||
合计 |
(2)已采用分层抽样的方式从样本的所有女生中抽取了5人，现从这5人中随机抽取2人参加座谈会，求抽到的2人恰好一文一理的概率。
| 0.15 | 0.10 | 0.05 | 0.01 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
（参考公式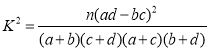
，其中
为样本容量）
【答案】（1）见解析；（2）
【解析】
（1）把数据填入列联表，计算
可得结论；
（2）抽取的5人中，文科女3人，理科女2人， 5人编号后用列举法列出任取2人的所有基本事件，并计算出抽到的2人恰好一文一理的事件数，然后由古典概型概率公式计算概率.
(1)列联表如下表:
男生 | 女生 | 合计 | |
文科 | 5 | 15 | 20 |
理科 | 30 | 10 | 40 |
合计 | 35 | 25 | 60 |
.所以有99.9%的把握认为二者有关；
(2)由题意知:抽取的5人中，文科女3人，理科女2人，分别设为
随机抽取2人，则共有: 
10种情况
其中，有6种情况符合题意，所以
. .
【题目】某地区某长产品近几年的产量统计如表：
年份 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
年份代码 | 1 | 2 | 3 | 4 | 5 | 6 |
年产量 | 6.6 | 6.7 | 7 | 7.1 | 7.2 | 7.4 |
（1）根据表中数据，建立
关于
的线性回归方程
；
（2）若近几年该农产品每千克的价格
（单位：元）与年产量满足的函数关系式为
，且每年该农产品都能售完.
①根据（1）中所建立的回归方程预测该地区2018（
）年该农产品的产量；
②当（
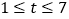）为何值时，销售额
最大？
附：对于一组数据
，
，…，
，其回归直线的斜率和截距的最小二乘估计分别为：
，
.
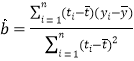【题目】下表为
年至
年某百货零售企业的线下销售额（单位：万元），其中年份代码
年份
．
年份代码 |
|
|
|
|
线下销售额 |
|
|
|
|
（1）已知
与
具有线性相关关系，求关于的线性回归方程，并预测
年该百货零售企业的线下销售额；
（2）随着网络购物的飞速发展，有不少顾客对该百货零售企业的线下销售额持续增长表示怀疑，某调查平台为了解顾客对该百货零售企业的线下销售额持续增长的看法，随机调查了
位男顾客、
位女顾客（每位顾客从“持乐观态度”和“持不乐观态度”中任选一种），其中对该百货零售企业的线下销售额持续增长持乐观态度的男顾客有
人、女顾客有
人，能否在犯错误的概率不超过
的前提下认为对该百货零售企业的线下销售额持续增长所持的态度与性别有关？
参考公式及数据：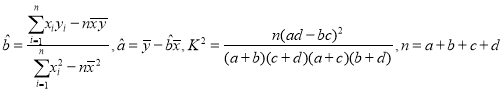
．
|
|
|
|
|
|
|
|
|
|
|
|
|
|
