题目内容
12.已知四边形ABCD中,∠ABC=∠ACB=58°,∠CAD=48°,∠BCD=30°,求∠BAD的度数.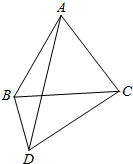
分析 先由三角形内角和为180°,求出∠BAC=180°-(∠ABC+∠ACB)=64°,再由∠BAD=∠BAC-∠CAD,能求出结果.
解答  解:四边形ABCD中,
解:四边形ABCD中,
∵∠ABC=∠ACB=58°,∠CAD=48°,∠BCD=30°,
∴∠BAC=180°-(∠ABC+∠ACB)=180°-(58°+58°)=64°,
∴∠BAD=∠BAC-∠CAD=64°-48°=16°.
点评 本题考查三角形内角度数的求法,是基础题,解题时要认真审题,注意三角形内角和定理的合理运用.

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
20.已知命题p:?x∈(0,+∞),x2≥x-1,则命题p的否定形式是( )
| A. | ¬p:?x0∈(0,+∞),x02≥x0-1 | B. | ¬p:?x0∈(-∞,+0),x02≥x0-1 | ||
| C. | ¬p:?x0∈(0,+∞),x02<x0-1 | D. | ¬p:?x0∈(-∞,+0),x02<x0-1 |
7.设F1,F2分别是双曲线$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的两个焦点,点A是以F1为圆心,b为半径的圆与双曲线的一个交点,且AF2与圆相切,则该双曲线的离心率为( )
| A. | 2$\sqrt{3}$ | B. | $\sqrt{3}$ | C. | 2$\sqrt{5}$ | D. | $\sqrt{5}$ |
4.函数y=loga(3x-2)+2的图象必过定点( )
| A. | (1,2) | B. | (2,2) | C. | (2,3) | D. | ($\frac{2}{3}$,2) |
2.已知函数f(x)=lnx+2的图象与直线y=x+a恰好有一个交点,设g(x)=ex-$\frac{1}{2}$x2-ax,当x∈[1,2]时,不等式-m≤g(x)≤m2-4恒成立,则实数m的取值范围是( )
| A. | (-∞,-e+$\frac{3}{2}$] | B. | [-e+$\frac{3}{2}$,e] | C. | [-e,e] | D. | [e,+∞) |
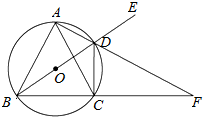 如图所示,⊙O为△ABC的外接圆,且AB=AC,过点A的直线交⊙O于D,交BC的延长线于F,DE是BD的延长线,连接CD.
如图所示,⊙O为△ABC的外接圆,且AB=AC,过点A的直线交⊙O于D,交BC的延长线于F,DE是BD的延长线,连接CD.