题目内容
6.已知a=log4$\frac{1}{3}$,b=lg5,c=${∫}_{0}^{1}$xdx,则实数a,b,c的大小关系为( )| A. | c<b<a | B. | c<a<b | C. | a<c<b | D. | a<b<c |
分析 先根据对数函数的性质得到a<0,b>$\frac{1}{2}$,再根据定积分的计算求得c=$\frac{1}{2}$,问题得以解决.
解答 解:a=log4$\frac{1}{3}$<0,b=lg5>lg$\sqrt{10}$=$\frac{1}{2}$,c=${∫}_{0}^{1}$xdx=$\frac{1}{2}$x2|${\;}_{0}^{1}$=$\frac{1}{2}$,
∴b>c>a,
故选:C.
点评 本题考查了对数函数的性质和定积分的计算,属于基础题.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
11.给出三条直线l1:4x+y=4,l2:mx+y=0,l3:2x-3my=4.
(1)m为何值时,三线共点;
(2)m=0时,三条直线能围成一个三角形吗?
(3)求当三条直线围成三角形时,m的取值范围.
(1)m为何值时,三线共点;
(2)m=0时,三条直线能围成一个三角形吗?
(3)求当三条直线围成三角形时,m的取值范围.
18.已知矩形ABCD,E、F分别是BC、AD的中点,且BC=2AB=2,现沿EF将平面ABEF折起,使平面ABEF⊥平面EFDC,则三棱锥A-FEC的外接球的体积为( )
| A. | $\frac{{\sqrt{3}}}{3}π$ | B. | $\frac{{\sqrt{3}}}{2}π$ | C. | $\sqrt{3}π$ | D. | $2\sqrt{3}π$ |
15.设集合S={y|y=3x,x∈R},T={y|y=x2+1,x∈R},则S∪T=( )
| A. | ∅ | B. | S | C. | T | D. | {0,1} |
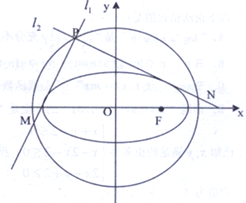 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的一个焦点F($\sqrt{2}$,0)其短轴上的一个端点到F的距离为$\sqrt{3}$
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的一个焦点F($\sqrt{2}$,0)其短轴上的一个端点到F的距离为$\sqrt{3}$ 如图,在平面直角坐标系xOy中,椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左右焦点分别为,F1和F2,上顶点为B,BF2,延长线交椭圆于点A,△ABF的周长为8,且$\overrightarrow{B{F_1}}•\overrightarrow{BA}$=0.
如图,在平面直角坐标系xOy中,椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左右焦点分别为,F1和F2,上顶点为B,BF2,延长线交椭圆于点A,△ABF的周长为8,且$\overrightarrow{B{F_1}}•\overrightarrow{BA}$=0.