题目内容
9．已知函数f（x）=lnx+x-2的零点x0∈[a，b]，且b-a=1，a，b∈N*，则a+b=（ ）| A． | 2 | B． | 3 | C． | 4 | D． | 5 |
分析 利用根的存在定理先判断函数零点所在的区间，然后确定与a，b的关系．
解答 解：因为f（x）=lnx+x-2，所以函数在定义域（0，+∞）上单调递增，
因为f（1）=ln1+1-2=-1＜0，f（2）=ln2+2-2=ln2＞0．
所以在区间[1，2]上，函数存在唯一的一个零点．
在由题意可知，a=1，b=2，所以a+b=3．
故选：B
点评 本题主要考查函数零点区间的判断以及根的存在性定理的应用，判断函数是单调增函数是解决本题的关键．
练习册系列答案
ABC考王全优卷系列答案
相关题目
19．设点A（-1，0），B（1，0），动点P到A点的距离与到B点的距离之比为2，则点P的轨迹方程是（ ）
| A． | ${（x-\frac{5}{3}）^2}+{y^2}=\frac{16}{9}$ | B． | ${（x+\frac{5}{3}）^2}+{y^2}=\frac{16}{9}$ | C． | ${（x-\frac{5}{3}）^2}+{y^2}=\frac{4}{3}$ | D． | ${（x+\frac{5}{3}）^2}+{y^2}=\frac{4}{3}$ |
17．函数f（x）在（-4，7）上是增函数，则使y=f（x-3）+2为增函数的区间为（ ）
| A． | （-2，3） | B． | （-1，7） | C． | （-1，10） | D． | （-10，-4） |
4．已知$\overrightarrow a=（x，2）$，$\overrightarrow b=（2，-1）$，$\overrightarrow a$∥$\overrightarrow b$，则$|\overrightarrow a+\overrightarrow b|$=（ ）
| A． | 2$\sqrt{5}$ | B． | 5 | C． | $\sqrt{10}$ | D． | $\sqrt{5}$ |
14．两条平行直线l1：3x-2y-1=0，l2：3x-2y+1=0的距离是（ ）
| A． | $\frac{{2\sqrt{13}}}{13}$ | B． | $\frac{{\sqrt{13}}}{13}$ | C． | $\frac{1}{13}$ | D． | $\frac{2}{13}$ |
18．
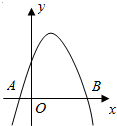如图所示为二次函数y=ax2+bx+c的图象，则|OA|•|OB|等于（ ）
如图所示为二次函数y=ax2+bx+c的图象，则|OA|•|OB|等于（ ）| A． | $\frac{c}{a}$ | B． | -$\frac{c}{a}$ | C． | ±$\frac{c}{a}$ | D． | -$\frac{a}{c}$ |