题目内容
13.已知向量$\overrightarrow{m}$=(3,cosx+$\frac{1}{3}$),$\overrightarrow{n}$=(3,sinx-$\frac{1}{3}$),x∈($\frac{3π}{4}$,$\frac{7π}{4}$),且$\overrightarrow{m}$∥$\overrightarrow{n}$,求$\frac{2+2tanx}{1-\sqrt{2}sin(2x+\frac{π}{4})}$的值.分析 由已知两向量共线求得$sin(x-\frac{π}{4})=\frac{\sqrt{2}}{3}$,结合给出角x的范围,利用配角方法求出sinx,cosx,tanx的值,化简$\frac{2+2tanx}{1-\sqrt{2}sin(2x+\frac{π}{4})}$后代值得答案.
解答 解:∵$\overrightarrow{m}$=(3,cosx+$\frac{1}{3}$),$\overrightarrow{n}$=(3,sinx-$\frac{1}{3}$),且$\overrightarrow{m}$∥$\overrightarrow{n}$,
∴3(sinx-$\frac{1}{3}$)-3(cosx+$\frac{1}{3}$)=0,
即3(sinx-cosx)=2,
$3\sqrt{2}sin(x-\frac{π}{4})=2$,
∴$sin(x-\frac{π}{4})=\frac{\sqrt{2}}{3}$.
∵x∈($\frac{3π}{4}$,$\frac{7π}{4}$),∴x-$\frac{π}{4}$∈($\frac{π}{2},\frac{3π}{2}$),
∴cos($x-\frac{π}{4}$)=-$\frac{\sqrt{7}}{3}$.
则sinx=sin[(x-$\frac{π}{4}$)+$\frac{π}{4}$]=sin(x-$\frac{π}{4}$)cos$\frac{π}{4}$+cos(x-$\frac{π}{4}$)sin$\frac{π}{4}$=$\frac{\sqrt{2}}{3}×\frac{\sqrt{2}}{2}-\frac{\sqrt{7}}{3}×\frac{\sqrt{2}}{2}$=$\frac{2-\sqrt{14}}{6}$.
cosx=cos[(x-$\frac{π}{4}$)+$\frac{π}{4}$]=cos(x-$\frac{π}{4}$)cos$\frac{π}{4}$-sin(x-$\frac{π}{4}$)sin$\frac{π}{4}$=$-\frac{\sqrt{7}}{3}×\frac{\sqrt{2}}{2}-\frac{\sqrt{2}}{3}×\frac{\sqrt{2}}{2}$=$\frac{-2-\sqrt{14}}{6}$.
∴tanx=$\frac{8-2\sqrt{14}}{5}$.
∴$\frac{2+2tanx}{1-\sqrt{2}sin(2x+\frac{π}{4})}$=$\frac{2+2tanx}{1-\sqrt{2}(sin2xcos\frac{π}{4}+cos2xsin\frac{π}{4})}$=$\frac{2+2tanx}{1-sin2x-cos2x}$
=$\frac{2+2×\frac{8-2\sqrt{14}}{5}}{1-2×\frac{2-\sqrt{14}}{6}×\frac{-2-\sqrt{14}}{6}-2×(\frac{-2-\sqrt{14}}{6})^{2}+1}$=$\frac{18-81\sqrt{14}}{50}$.
点评 本题考查向量共线的坐标表示,考查了三角函数的化简与求值,训练了拆角配角思想在解题中的应用,属中档题.

| A. | 四棱柱 | B. | 四棱锥 | C. | 四棱台 | D. | 五棱柱 |
| A. | 1 | B. | 3 | C. | 10 | D. | 13 |
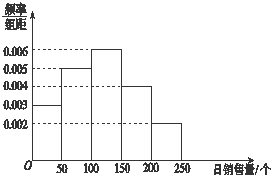 一家企业据以往某种新产品的销售记录,绘制了日销售量的频率分布直方图,如图所示.由频率分布直方图,估计这种新产品的日销售量的中位数为117.(结果保留整数)
一家企业据以往某种新产品的销售记录,绘制了日销售量的频率分布直方图,如图所示.由频率分布直方图,估计这种新产品的日销售量的中位数为117.(结果保留整数)