题目内容
14.下图是函数f(x)=Asinωx(A>0,ω>0)一个周期的图象,则f(1)+f(2)+f(3)+f(4)+f(5)+f(6)的值等于( )
| A. | $\sqrt{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | 2+$\sqrt{2}$ | D. | 2$\sqrt{2}$ |
分析 根据f(x)=Asinωx的周期性求出ω的值,可得f(x)的解析式,分别求得f(1)、f(2)、f(3)、f(4)、f(5)、f(6)的值,可得要求式子的值.
解答 解:根据函数f(x)=Asinωx(A>0,ω>0)一个周期的图象,
可得A=2,周期等于$\frac{2π}{ω}$=8,∴ω=$\frac{π}{4}$,f(x)=2sin($\frac{π}{4}$x),
故f(1)=$\sqrt{2}$,f(2)=2,f(3)=$\sqrt{2}$,f(4)=0,
f(5)=-$\sqrt{2}$,f(6)=-2,
∴f(1)+f(2)+f(3)+f(4)+f(5)+f(6)=$\sqrt{2}$,
故选:A.
点评 本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,求函数的值,属于基础题.

练习册系列答案
 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
6.已知F1、F2为椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{169}$=1的两个焦点,过F1的直线交椭圆于A、B两点.若|F2A|+|F2B|=30,则|AB|=( )
| A. | 16 | B. | 18 | C. | 22 | D. | 20 |
3.执行如图的程序框图,若输出的k=2,则输入x的取值范围是( )
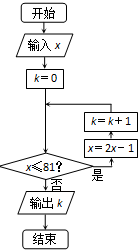

| A. | (21,41) | B. | [21,41] | C. | (21,41] | D. | [21,41) |