题目内容
已知函数f(x)=-1+2
sinxcosx+2cos2x,
(1)求函数f(x)的最小正周期;
(2)求函数f(x)的单调减区间;
(3)画出函数g(x)=f(x),x∈[-
,
]的图象,由图象研究并写出g(x)的对称轴和对称中心.

| 3 |
(1)求函数f(x)的最小正周期;
(2)求函数f(x)的单调减区间;
(3)画出函数g(x)=f(x),x∈[-
| 7π |
| 12 |
| 5π |
| 12 |

(1)f(x)=
sin2x+cos2x=2sin(2x+
),周期 T=
=π.
(2)由
+2kπ≤2x+
≤
+2kπ(k∈Z),得
+kπ≤x≤
+kπ,
所以,减区间为[
+kπ,
+kπ](k∈Z).
(3)如图所示:g(x)无对称轴,对称中心为(-
,0).

| 3 |
| π |
| 6 |
| 2π |
| 2 |
(2)由
| π |
| 2 |
| π |
| 6 |
| 3π |
| 2 |
| π |
| 6 |
| 2π |
| 3 |
所以,减区间为[
| π |
| 6 |
| 2π |
| 3 |
(3)如图所示:g(x)无对称轴,对称中心为(-
| π |
| 12 |


练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目




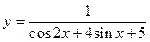 的值域是 .
的值域是 . 的三个内角的余弦值分别等于
的三个内角的余弦值分别等于 三个内角的正弦值,则( )
三个内角的正弦值,则( )
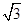



 ,则
,则 ( )
( )


