题目内容
【题目】已知椭圆![]() ,过点
,过点![]() 作椭圆C的切线l,在第一象限的切点为P,过点P作与直线l倾斜角互补的直线,恰好经过椭圆C的下顶点N.
作椭圆C的切线l,在第一象限的切点为P,过点P作与直线l倾斜角互补的直线,恰好经过椭圆C的下顶点N.
(1)求椭圆C的方程;
(2)F为椭圆C的右焦点,过点F且与x轴不垂直的直线![]() 交椭圆C于A,B两点,点A关于x轴的对称点为
交椭圆C于A,B两点,点A关于x轴的对称点为![]() ,则直线
,则直线![]() 是否过定点,若是,求出定点坐标;若不是,请说明理由.
是否过定点,若是,求出定点坐标;若不是,请说明理由.
【答案】(1)![]() (2)
(2)![]() 过定点
过定点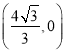 .
.
【解析】
(1)设出直线l的方程,联立直线与椭圆方程,利用相切得到根的判别式为0,进而得到切点坐标,再根据两直线倾斜角之间的关系,得到b的值,从而得椭圆C的方程;(2)设出直线![]() 的方程,联立直线与椭圆方程,设出
的方程,联立直线与椭圆方程,设出![]() ,
,![]() ,可得
,可得![]() ,
,![]() 及
及![]() 坐标,写出直线
坐标,写出直线![]() 的方程,化简,根据方程的特点,即得
的方程,化简,根据方程的特点,即得![]() 过定点
过定点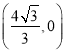 .
.
解:(1)由题意可知直线l的斜率存在且不为0,设直线l的方程为![]() ,与椭圆方程联立,得
,与椭圆方程联立,得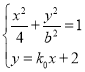 ,化简整理得
,化简整理得![]() ,(*)
,(*)
![]() ,得
,得![]() ,
,
所以方程(*)可化为![]() ,可得切点
,可得切点![]() .
.
![]() ,由已知
,由已知![]() ,
,
所以![]() ,即
,即![]() ,得
,得![]() ,
,
所以椭圆C的方程为![]() .
.
(2)由(1)知![]() ,
,
设直线![]() 的方程为
的方程为![]() ,与椭圆方程联立,得
,与椭圆方程联立,得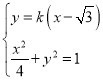 ,化简整理得
,化简整理得![]() ,
,
设![]() ,
,![]() ,则
,则![]() ,
,![]() .
.
由![]() ,可得
,可得![]() ,则
,则
![]() 的方程为
的方程为![]() ,
,
即![]()
![]()
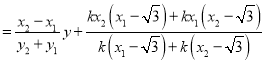
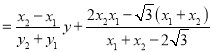
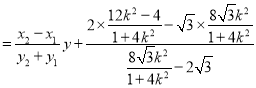
![]() ,
,
所以当![]() 时,
时,![]() ,即
,即![]() 过定点
过定点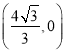 .
.
拓展结论:
圆![]() 上点
上点![]() 处的切线方程为
处的切线方程为![]() ,而若点
,而若点![]() 在圆外,则直线方程
在圆外,则直线方程![]() 的几何含义是过点
的几何含义是过点![]() 所作圆的两条切线的切点连线的方程;由此类比:椭圆
所作圆的两条切线的切点连线的方程;由此类比:椭圆![]() 上点
上点![]() 处的切线方程为
处的切线方程为![]() ,而若点
,而若点![]() 在椭圆外,则方程
在椭圆外,则方程![]() 的几何含义是过点
的几何含义是过点![]() 所作椭圆的两条切线的切点连线的方程;抛物线
所作椭圆的两条切线的切点连线的方程;抛物线![]() 上点
上点![]() 处的切线方程为
处的切线方程为![]() ,而若点
,而若点![]() 在抛物线外,则直线方程
在抛物线外,则直线方程![]() 的几何含义是过点
的几何含义是过点![]() 所作抛物线的两条切线的切点连线的方程.
所作抛物线的两条切线的切点连线的方程.

练习册系列答案
相关题目