МвДҝДЪИЭ
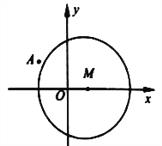
ЎҫМвДҝЎҝТСЦӘAЈЁx0 Ј¬ 0Ј©Ј¬BЈЁ0Ј¬y0Ј©БҪөг·ЦұрФЪxЦбәНyЦбЙПФЛ¶ҜЈ¬ЗТ|AB|=1Ј¬Иф¶ҜөгPЈЁxЈ¬yЈ©ВъЧг ![]() Ј®
Ј®
ЈЁ1Ј©Зуіц¶ҜөгPөД№мјЈ¶ФУҰЗъПЯCөДұкЧј·ҪіМЈ»
ЈЁ2Ј©Т»МхЧЭҪШҫаОӘ2өДЦұПЯl1УлЗъПЯCҪ»УЪPЈ¬QБҪөгЈ¬ИфТФPQЦұҫ¶өДФІЗЎ№эФӯөгЈ¬ЗуіцЦұПЯ·ҪіМЈ»
ЈЁ3Ј©ЦұПЯl2Јәx=ty+1УлЗъПЯCҪ»УЪAЎўBБҪөгЈ¬EЈЁ1Ј¬0Ј©Ј¬КФОКЈәөұtұд»ҜКұЈ¬КЗ·сҙжФЪТ»ЦұПЯl2 Ј¬ К№ЎчABEөДГж»эОӘ ![]() ЈҝИфҙжФЪЈ¬ЗуіцЦұПЯl2өД·ҪіМЈ»ИфІ»ҙжФЪЈ¬ЛөГчАнУЙЈ®
ЈҝИфҙжФЪЈ¬ЗуіцЦұПЯl2өД·ҪіМЈ»ИфІ»ҙжФЪЈ¬ЛөГчАнУЙЈ®
Ўҫҙр°ёЎҝ
ЈЁ1Ј©ҪвЈәТтОӘ ![]() Ј¬
Ј¬
јҙ ![]() Ј¬
Ј¬
ЛщТФ ![]() Ј¬
Ј¬
ЛщТФ ![]()
УЦТтОӘ|AB|=1Ј¬ЛщТФ ![]() Ј¬
Ј¬
јҙЈә ![]() Ј¬
Ј¬
јҙ ![]() Ј¬
Ј¬
ЛщТФНЦФІөДұкЧј·ҪіМОӘ ![]() Ј®
Ј®
ЈЁ2Ј©ҪвЈәЦұПЯl1РұВКұШҙжФЪЈ¬ЗТЧЭҪШҫаОӘ2Ј¬ЙиЦұПЯОӘy=kx+2БӘБўЦұПЯl1әННЦФІ·ҪіМ 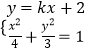 Ј¬
Ј¬
өГЈәЈЁ3+4k2Ј©x2+16kx+4=0Ј¬
УЙЎчЈҫ0Ј¬өГ ![]() ЈЁ*Ј©Ј¬
ЈЁ*Ј©Ј¬
ЙиPЈЁx1Ј¬y1Ј©Ј¬QЈЁx2Ј¬y2Ј©Ј¬
Фт ![]() ЈЁ1Ј©
ЈЁ1Ј©
ТФPQЦұҫ¶өДФІЗЎ№эФӯөгЈ¬
ЛщТФOPЎНOQЈ¬ ![]() Ј¬
Ј¬
јҙx1x2+y1y2=0Ј¬
ТІјҙx1x2+ЈЁkx1+2Ј©ЈЁkx2+2Ј©=0Ј¬
јҙЈЁ1+k2Ј©x1x2+2kЈЁx1+x2Ј©+4=0Ј¬
Ҫ«ЈЁ1Ј©КҪҙъИлЈ¬өГ ![]() ©Ғ
©Ғ ![]() +4=0Ј¬
+4=0Ј¬
јҙ4ЈЁ1+k2Ј©©Ғ32k2+4ЈЁ3+4k2Ј©=0Ј¬
ҪвөГ ![]() Ј¬ВъЧгЈЁ*Ј©КҪЈ¬
Ј¬ВъЧгЈЁ*Ј©КҪЈ¬
ЛщТФ ![]() Ј®
Ј®
ЛщТФЦұПЯ·ҪіМОӘy=ЎА ![]() x+2
x+2
ЈЁ3Ј©ҪвЈәУЙ·ҪіМЧй 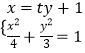 Ј¬өГЈЁ3t2+4Ј©y2+6ty©Ғ9=0ЈЁ*Ј©
Ј¬өГЈЁ3t2+4Ј©y2+6ty©Ғ9=0ЈЁ*Ј©
ЙиAЈЁx1Ј¬y1Ј©Ј¬BЈЁx2Ј¬y2Ј©Ј¬
Фт ![]()
ЛщТФ ![]() Ј¬
Ј¬
ТтОӘЦұПЯlЈәx=ty+1№эөгFЈЁ1Ј¬0Ј©Ј¬
ЛщТФSЎчABE= ![]() |EF||y1©Ғy2|=
|EF||y1©Ғy2|= ![]() ЎБ2ЎБ
ЎБ2ЎБ ![]() =
= ![]()
Бо= ![]() =2
=2 ![]() Ј¬Фт
Ј¬Фт ![]() І»іЙБў
І»іЙБў
№КІ»ҙжФЪЦұПЯlВъЧгМвТв
ЎҫҪвОцЎҝЈЁ1Ј©ёщҫЭПтБҝөДЧшұкФЛЛгЈ¬ТФј°|AB|=1Ј¬өГөҪНЦФІөДұкЧј·ҪіМОӘ ![]() Ј®ЈЁ2Ј©ЦұПЯl1РұВКұШҙжФЪЈ¬ЗТЧЭҪШҫаОӘ2Ј¬ёщҫЭЦұПЯУлНЦФІөДО»ЦГ№ШПөЈ¬јҙҝЙЗуіцkөДЦөЈ¬ОКМвөГТФҪвҫцЈ®ЈЁ3Ј©ёщҫЭЦұПЯәННЦФІ¶оО»ЦГ№ШПөЈ¬ТФј°ИэҪЗРОөДГж»э№«КҪөГөҪSЎчABE=
Ј®ЈЁ2Ј©ЦұПЯl1РұВКұШҙжФЪЈ¬ЗТЧЭҪШҫаОӘ2Ј¬ёщҫЭЦұПЯУлНЦФІөДО»ЦГ№ШПөЈ¬јҙҝЙЗуіцkөДЦөЈ¬ОКМвөГТФҪвҫцЈ®ЈЁ3Ј©ёщҫЭЦұПЯәННЦФІ¶оО»ЦГ№ШПөЈ¬ТФј°ИэҪЗРОөДГж»э№«КҪөГөҪSЎчABE= ![]() Ј¬Бо=
Ј¬Бо= ![]() =2
=2 ![]() Ј¬Фт
Ј¬Фт ![]() І»іЙБўЈ¬ОКМвөГТФҪвҫцЈ®
І»іЙБўЈ¬ОКМвөГТФҪвҫцЈ®

ЎҫМвДҝЎҝДіПШҪМУэҫЦОӘБЛјмІйұҫПШјЧЎўТТБҪЛщѧУөДС§Йъ¶Ф°ІИ«ЦӘК¶өДС§П°ЗйҝцЈ¬ФЪХвБҪЛщѧУҪшРРБЛ°ІИ«ЦӘК¶ІвКФЈ¬Лж»ъФЪХвБҪЛщѧУёчійИЎ20ГыС§ЙъөДҝјКФіЙјЁЧчОӘСщұҫЈ¬іЙјЁҙуУЪ»төИУЪ80·ЦөДОӘУЕРгЈ¬·сФтОӘІ»УЕРгЈ¬НіјЖҪб№ыИзПВНјЈә


јЧРЈ ТТРЈ
ЈЁ1Ј©ҙУТТРЈіЙјЁУЕРгөДС§ЙъЦРИОСЎБҪГыЈ¬ЗуХвБҪГыС§ЙъөДіЙјЁЗЎУРТ»ёцВдФЪ![]() ДЪөДёЕВКЈ»
ДЪөДёЕВКЈ»
ЈЁ2Ј©УЙТФЙПКэҫЭНкіЙПВГжБРБӘұнЈ¬Іў»ШҙрДЬ·сФЪ·ёҙнөДёЕВКІ»і¬№э0.1өДЗ°МбПВИПОӘС§ЙъөДіЙјЁУлБҪЛщѧУөДСЎФсУР№ШЎЈ
јЧРЈ | ТТРЈ | ЧЬјЖ | |
УЕРг | |||
І»УЕРг | |||
ЧЬјЖ |
![]()
ІОҝјКэҫЭ | PЈЁK2ЎЭk0Ј© | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.706 | span>3.841 | 5.024 | 6.635 | 7.879 | 10.828 |