题目内容
已知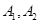 为椭圆
为椭圆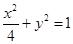 的左右顶点,在长轴
的左右顶点,在长轴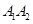 上随机任取点
上随机任取点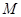 ,过
,过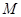 作垂直于
作垂直于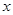 轴的直线交椭圆于点
轴的直线交椭圆于点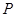 ,则使
,则使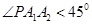 的概率为
的概率为
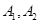 为椭圆
为椭圆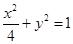 的左右顶点,在长轴
的左右顶点,在长轴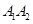 上随机任取点
上随机任取点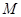 ,过
,过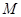 作垂直于
作垂直于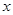 轴的直线交椭圆于点
轴的直线交椭圆于点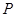 ,则使
,则使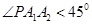 的概率为
的概率为A. | B. | C. | D. |
A
试题分析:椭圆的长轴长为4,设M(m,0),P(m,n)(-2<m<0),则当
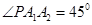 时,
时,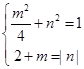 ,解得,
,解得,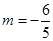 ,所以,
,所以,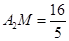 ,故当点M落在
,故当点M落在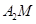 上时,满足
上时,满足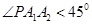 ,因此,使
,因此,使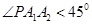 的概率为
的概率为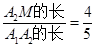 ,选A。
,选A。点评:小综合题,几何概型概率的计算,关键是弄清“两个几何度量”,本题结合点P在椭圆的位置,从确定使
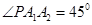 的点M入手,得到几何度量。
的点M入手,得到几何度量。
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 中,
中, 且
且 ,
, . 以
. 以 ,
, 为焦点,且过点
为焦点,且过点 的双曲线的离心率为
的双曲线的离心率为 ;以
;以 ,
, ,则
,则 的取值范围为( )
的取值范围为( )




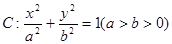 ,
,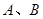 是长轴的左、右端点,动点
是长轴的左、右端点,动点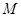 满足
满足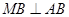 ,联结
,联结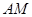 ,交椭圆于点
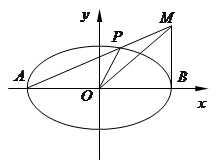
,交椭圆于点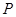 .
. 
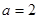 ,
,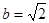 时,设
时,设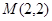 ,求
,求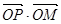 的值;
的值;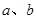 满足的条件?并说明理由;
满足的条件?并说明理由; 的离心率为 ( )
的离心率为 ( )



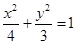 的左焦点为
的左焦点为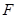 ,过点
,过点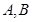 两点,线段
两点,线段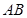 的中点为
的中点为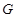 ,
,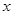 轴和
轴和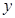 轴分别交于
轴分别交于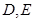 两点.
两点.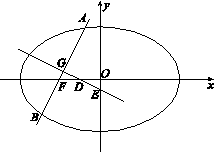
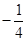 ,求直线
,求直线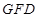 的面积为
的面积为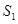 ,△
,△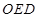 (
(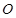 为原点)的面积为
为原点)的面积为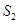 .试问:是否存在直线
.试问:是否存在直线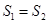 ?说明理由.
?说明理由.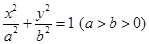 过点
过点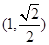 ,离心率为
,离心率为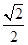 ,左、右焦点分别为
,左、右焦点分别为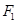 、
、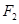 .点
.点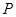 为直线
为直线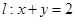 上且不在
上且不在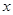 轴上的任意一点,直线
轴上的任意一点,直线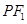 和
和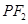 与椭圆的交点分别为
与椭圆的交点分别为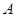 、
、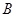 和
和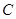 、
、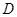 ,
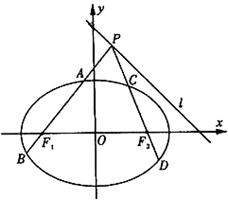
,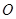 为坐标原点.设直线
为坐标原点.设直线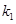 、
、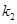 .
.
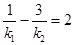 ;
;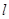 上是否存在点
上是否存在点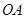 、
、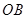 、
、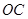 、
、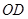 的斜率
的斜率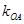 、
、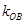 、
、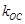 、
、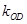 满足
满足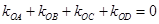 ?若存在,求出所有满足条件的点
?若存在,求出所有满足条件的点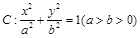 ,直线l为圆
,直线l为圆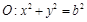 的一条切线,且经过椭圆C的右焦点,直线l的倾斜角为
的一条切线,且经过椭圆C的右焦点,直线l的倾斜角为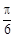 ,记椭圆C的离心率为e.
,记椭圆C的离心率为e.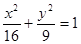 的焦距是 ,焦点坐标为
的焦距是 ,焦点坐标为 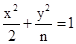 的离心率为
的离心率为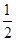 ,则n=( )
,则n=( )


