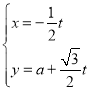��Ŀ����
����Ŀ����������ѧУ�����꼶�ֱ���1100�ˣ�1000�ˣ�Ϊ���˽�����ѧУȫ������꼶ѧ���ڸõ���һģ���Ե���ѧ�ɼ���������÷ֲ��������������ѧУһ����ȡ��105��ѧ������ѧ�ɼ�����������Ƶ���ֲ�ͳ�Ʊ����£�

��1������![]() ��
��![]() ��ֵ��
��ֵ��
��2�����涨���Գɼ���![]() Ϊ���㣬���������������У��ѧ�ɼ��������ʣ�
Ϊ���㣬���������������У��ѧ�ɼ��������ʣ�
��3�����涨���Գɼ���![]() ��Ϊ���㣬������ͳ��������д����
��Ϊ���㣬������ͳ��������д����![]() �������������Ƿ��������жϣ��Ƿ���
�������������Ƿ��������жϣ��Ƿ���![]() �İ�����Ϊ����ѧУ����ѧ�ɼ��в���.
�İ�����Ϊ����ѧУ����ѧ�ɼ��в���.

����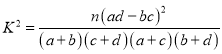 ��
��![]() .
.
![]()
���𰸡���1��![]() ��
��![]() ����2��
����2��![]() ����3����95���İ�����Ϊ����ѧУ��ѧ�ɼ��в���
����3����95���İ�����Ϊ����ѧУ��ѧ�ɼ��в���
��������
��1���ɷֲ������֪ʶ�������������ݷֱ�������У����У��ȡ���������ɵ�![]() ��
��![]() ��ֵ��
��ֵ��
��2�����������������ʣ��ɵ���У�������ʣ�
��3����ȫ![]() �������������
�������������![]() ��ֵ�������ٽ���ɵô�.
��ֵ�������ٽ���ɵô�.
�⣺��1��������֪��
��У��ȡ![]() �ˣ���
�ˣ���![]() ��
��
��У��ȡ![]() �ˣ���
�ˣ���![]() .
.
��2��������֪����У������Ϊ![]() .
.
��3��������±���1��.
��У | ��У | �ܼ� | |
���� | 10 | 20 | 30 |
������ | 45 | 30 | 75 |
�ܼ� | 55 | 50 | 105 |
��������![]() ��
��
���������ݵã���95���İ�����Ϊ����ѧУ��ѧ�ɼ��в���.

 ����ͼ����ּ��������ҵ֣�ݴ�ѧ������ϵ�д�
����ͼ����ּ��������ҵ֣�ݴ�ѧ������ϵ�д�����Ŀ��Ϊ�˽�ס������̷۳��IJ�Ʒ���������÷ֲ�����ķ����Ӽס������̷۳������IJ�Ʒ�зֱ��ȡ16����5����������Ʒ����Ԫ��![]() �ĺ�������λ�����ˣ����±����ҳ���5����Ʒ�IJ������ݣ�
�ĺ�������λ�����ˣ����±����ҳ���5����Ʒ�IJ������ݣ�
��� | 1 | 2 | 3 | 4 | 5 |
| 170 | 178 | 166 | 176 | 180 |
| 74 | 80 | 77 | 76 | 81 |
��1����֪�׳������IJ�Ʒ����96�������ҳ������IJ�Ʒ������
��2������Ʒ�е���Ԫ��![]() ����
����![]() ��
��![]() ʱ���ò�ƷΪ�ŵ�Ʒ���������������ݹ����ҳ��������ŵ�Ʒ��������
ʱ���ò�ƷΪ�ŵ�Ʒ���������������ݹ����ҳ��������ŵ�Ʒ��������
��3�����ҳ����������5����Ʒ�У������ȡ2�������ȡ��2����Ʒ���ŵ�Ʒ��![]() �ķֲ��м����ֵ������ѧ��������
�ķֲ��м����ֵ������ѧ��������