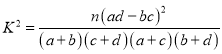题目内容
【题目】已知函数f(x)=ax﹣cosx,a≠0.
(1)若函数f(x)为单调函数,求a的取值范围;
(2)若x∈[0,2π],求:当a≥![]() 时,函数f(x)仅有一个零点.
时,函数f(x)仅有一个零点.
【答案】(1)![]() 或
或![]() (2)详见解析
(2)详见解析
【解析】
(1)首先求函数的导数,![]() ,当函数单调递增时
,当函数单调递增时![]() 恒成立,当函数单调递减时,
恒成立,当函数单调递减时,![]() 恒成立;(2)根据(1)可知当
恒成立;(2)根据(1)可知当![]() 时,函数单调递增,根据零点存在性定理可知只有一个交点,当
时,函数单调递增,根据零点存在性定理可知只有一个交点,当![]() 时,可得函数存在两个极值点,
时,可得函数存在两个极值点,![]() ,根据单调性可判断,
,根据单调性可判断,![]() 是极大值,
是极大值,![]() 是极小值,因为
是极小值,因为![]() ,
,![]() ,若函数只有一个零点,只需满足
,若函数只有一个零点,只需满足![]() ,即可求得
,即可求得![]() 的取值范围.
的取值范围.
(1)解:由![]() ,可得
,可得![]() ,
,![]() .
.
因为![]() ,
,
所以当![]() 时,
时,![]() ,
,![]() 为
为![]() 上的单调增函数;
上的单调增函数;
当![]() 时,
时,![]() ,
,![]() 为
为![]() 上的单调减函数.
上的单调减函数.
综上,若函数![]() 为单调函数,则
为单调函数,则![]() 或
或![]() .
.
(2)证明:当![]() 时,由(1)可知
时,由(1)可知![]() 为
为![]() 上的单调增函数.
上的单调增函数.
又![]() ,
,![]()
所以函数![]() 在
在![]() 有且仅有一个零点,满足题意.
有且仅有一个零点,满足题意.
当![]() 时,
时,
令![]() ,则
,则![]() .由于
.由于![]() ,所以
,所以![]() ,
,
从而必有![]() ,
,![]() ,使
,使![]() ,且
,且![]() .
.
不妨设![]() ,且有
,且有![]() ,
,![]() ,
,
所以当![]() 时,
时,![]() ,
,![]() 为增函数;
为增函数;
当![]() 时,
时,![]() ,
,![]() 为减函数;
为减函数;
当![]() 时,
时,![]() ,
,![]() 为增函数.
为增函数.
从而函数![]() 的极大值为
的极大值为![]() ,极小值为
,极小值为![]() .
.
因为![]() ,所以
,所以![]() ,从而极大值
,从而极大值![]() .
.
又![]() ,
,
要使函数![]() 仅有一个零点,则极小值
仅有一个零点,则极小值![]() ,
,
所以![]() ,即
,即![]() .
.
又![]() ,
,![]() ,
,
所以当![]() 时,函数
时,函数![]() 仅有一个零点.
仅有一个零点.

【题目】为了检验“喜欢玩手机游戏与认为作业多”是否有关系,某班主任对班级的30名学生进行了调查,得到一个![]() 列联表:
列联表:
认为作业多 | 认为作业不多 | 合计 | |
喜欢玩手机游戏 | 18 | 2 | |
不喜欢玩手机游戏 | 6 | ||
合计 | 30 |
(1)请将上面的列联表补充完整(在答题卡上直接填写结果,不需要写求解过程);
(2)能否在犯错误的概率不超过0.005的前提下认为“喜欢玩手机游戏”与“认为作业多”有关系?
(3)若从不喜欢玩手机游戏的人中随机抽取3人,则至少2人认为作业不多的概率是多少?
参考公式及参考数据:独立性检验概率表
P( | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.83 |
计算公式: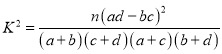
【题目】某市调研考试后,某校对甲、乙两个文科班的数学考试成绩进行分析,规定:大于或等于120分为优秀,120分以下为非优秀.统计成绩后,得到如下的列联表,且已知在甲、乙两个文科班全部110人中优秀的人数是30人.
(1)请完成上面的列联表;
优秀 | 非优秀 | 合计 | |
甲班 | 10 | ||
乙班 | 30 | ||
合计 | 110 |
(2)根据列联表的数据,若按99.9%的可靠性要求,能否认为“成绩与班级有关系”;
参考公式与临界值表![]() .
.
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |