题目内容
已知双曲线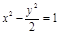 的焦点为F1.F2,点M在双曲线上且
的焦点为F1.F2,点M在双曲线上且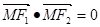 ,则点M到x轴的距离为 ( )
,则点M到x轴的距离为 ( )
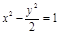 的焦点为F1.F2,点M在双曲线上且
的焦点为F1.F2,点M在双曲线上且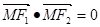 ,则点M到x轴的距离为 ( )
,则点M到x轴的距离为 ( )A.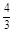 | B.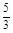 | C.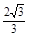 | D.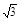 |
C
试题分析:a=1,b=
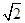 ,c=
,c=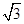 ;
;因为
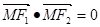 ,所以
,所以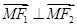 ,设
,设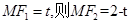
在直角三角形
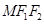 中,有
中,有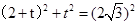 ,t=
,t=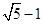 ,由
,由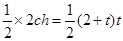 得h=
得h=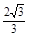 ,故选C。
,故选C。点评:基础题,紧扣双曲线的定义,注意运用“等面积法”求点M到x轴的距离。

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目
题目内容
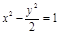 的焦点为F1.F2,点M在双曲线上且
的焦点为F1.F2,点M在双曲线上且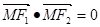 ,则点M到x轴的距离为 ( )
,则点M到x轴的距离为 ( )A.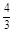 | B.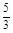 | C.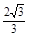 | D.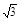 |
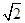 ,c=
,c=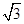 ;
;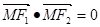 ,所以
,所以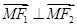 ,设
,设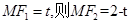
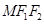 中,有
中,有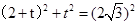 ,t=
,t=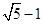 ,由
,由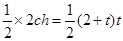 得h=
得h=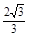 ,故选C。
,故选C。
 全能测控一本好卷系列答案
全能测控一本好卷系列答案