题目内容
已知正方形ABCD的边长为2,E,F,G,H分别是边AB,BC,CD,DA的中点.
(1)从C,D,E,F,G,H这六个点中,随机选取两个点,记这两个点之间的距离的平方为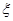 ,求概率P
,求概率P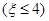 .
.
(2)在正方形ABCD内部随机取一点P,求满足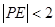 的概率.
的概率.
(1)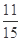 ;(2)
;(2) 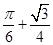
解析试题分析:(1)依题意由六个点中任取两个点共有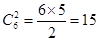 种情况,而其中两个点之间的距离的平方大于4的情况有4种,所以符合题意的共有11种,即可得到结论.本小题考查古典概型的问题,“正难则反”,也是这类题中的一种解题方法.
种情况,而其中两个点之间的距离的平方大于4的情况有4种,所以符合题意的共有11种,即可得到结论.本小题考查古典概型的问题,“正难则反”,也是这类题中的一种解题方法.
(2)因为正方形ABCD内部随机取一点P,则满足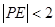 的概率,即需要求出点P所围成的面积,通过求出一个扇形与两个直角三角形的面积和,即可求得结论.
的概率,即需要求出点P所围成的面积,通过求出一个扇形与两个直角三角形的面积和,即可求得结论.
试题解析:(1)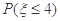 =
=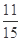
(2)这是一个几何概型.所有点 构成的平面区域是正方形
构成的平面区域是正方形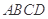 的内部,其面积是
的内部,其面积是 .满足
.满足 的点
的点 构成的平面区域是以
构成的平面区域是以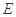 为圆心,2为半径的圆的内部与正方形
为圆心,2为半径的圆的内部与正方形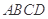 内部的公共部分,它可以看作是由一个以
内部的公共部分,它可以看作是由一个以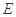 为圆心、2为半径、圆心角为
为圆心、2为半径、圆心角为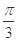 的扇形的内部与两个直角边分别为1和
的扇形的内部与两个直角边分别为1和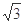 的直角三角形内部构成.其面积是
的直角三角形内部构成.其面积是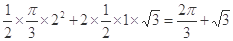 .
.
所以满足 的概率为
的概率为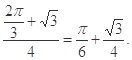
考点:1.古典概型的知识.2.几何概型的知识.3.正难则反推理的数学思想.

练习册系列答案
相关题目
年龄在60岁(含60岁)以上的人称为老龄人,某地区老龄人共有35万,随机调查了该地区700名老龄人的健康状况,结果如下表:
| 健康指数 | 2 | 1 | 0 | -1 |
| 60岁至79岁的人数 | 250 | 260 | 65 | 25 |
| 80岁及以上的人数 | 20 | 45 | 20 | 15 |
(1)估计该地区80岁以下老龄人生活能够自理的概率。
(2)若一个地区老龄人健康指数的平均值不小于1.2,则该地区可被评为“老龄健康地区”.
请写出该地区老龄人健康指数X分布列,并判断该地区能否被评为“老龄健康地区”.
甲、乙两药厂生产同一型号药品,在某次质量检测中,两厂各有5份样品送检,检测的平均得分相等(检测满分为100分,得分高低反映该样品综合质量的高低).成绩统计用茎叶图表示如下:
| 甲 | | 乙 |
| 9 8 | 8 | 4 8 9 |
| 2 1 0 | 9 | 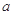 6 6 |
(1)求
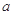 ;
;(2)某医院计划采购一批该型号药品,从质量的稳定性角度考虑,你认为采购哪个药厂的产品
比较合适?
(3)检测单位从甲厂送检的样品中任取两份作进一步分析,在抽取的两份样品中,求至少有一份得分在(90,100]之间的概率.
对一批共50件的某电器进行分类检测,其重量(克)统计如下:
| 重量段 | [80,85) | [85,90) | [90,95) | [95,100] |
| 件数 | 5 | a | 15 | b |
(1)从该批电器中任选1件,求其为“B”型的概率;
(2)从重量在[80,85)的5件电器中,任选2件,求其中恰有1件为“A”型的概率.
 ,
, ;两小时以上且不超过三小时还车的概率分别为
;两小时以上且不超过三小时还车的概率分别为 的概率.
的概率.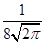 .
.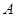 、
、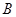 、
、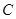 三道工序加工而成的,
三道工序加工而成的, 、
、 、
、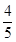 .已知每道工序的加工都相互独立,三道工序加工的产品都为合格时产品为一等品;恰有两次合格为二等品;其它的为废品,不进入市场.
.已知每道工序的加工都相互独立,三道工序加工的产品都为合格时产品为一等品;恰有两次合格为二等品;其它的为废品,不进入市场. 为三道加工工序中产品合格的工序数,求
为三道加工工序中产品合格的工序数,求