题目内容
一个袋中装有四个形状大小完全相同的球,球的编号分别为1,2,3,4.
(1)从袋中随机抽取两个球,求取出的球的编号之和不大于4的概率;
(2)先从袋中随机取一个球,该球的编号为m,将球放回袋中,然后再从袋中随机取一个球,该球的编号为n,求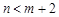 的概率.
的概率.
(1)取出的球的编号之和不大于4的概率为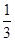 ;(2)
;(2)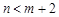 的概率为
的概率为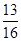 .
.
解析试题分析:本小题主要考察古典概型、对立事件的概率计算,考察学生分析问题 、解决问题的能力;先列举出所有可能的结果,再找出满足条件的有几种,两者相比即可.
试题解析:(1)从袋子中随机取两个球,其一切可能的结果组成的基本事件有1和2,1和3,1和4,2
和3,2和4,3和4,共6个;
从袋中随机取出的球的编号之和不大于4的事件共有1和2,1和3两个;
因此所求事件的概率为1/3.
(2)先从袋中随机取一个球,记下编号为m,放回后,在从袋中随机取一个球,记下编号为n,其一切可能的结果(m, n)有:
(1,1)(1,2),(1,3),(1,4),(2,1),(2,2),(2,3),(2,4),(3,1)(3,2), (3,3) (3,4),(4,1) (4,2),(4,3)(4,4),共16个
有满足条件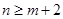 的事件为(1,3) (1,4) (2,4),共3个
的事件为(1,3) (1,4) (2,4),共3个
所以满足条件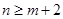 的事件的概率为
的事件的概率为 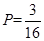 .
.
故满足条件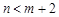 的事件的概率为
的事件的概率为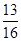 .
.
考点:古典概型、对立事件的概率.

 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案某农场计划种植某种新作物,为此对这种作物的两个品种(分别称为品种甲和品种乙)进行田间试验.选取两大块地,每大块地分成n小块地,在总共2n小块地中,随机选n小块地种植品种甲,另外n小块地种植品种乙.
(1)假设n=4,在第一大块地中,种植品种甲的小块地的数目记为X,求X的分布列和数学期望;
(2)试验时每大块地分成8小块,即n=8,试验结束后得到品种甲和品种乙在各小块地上的每公顷产量(单位:kg/hm2)如下表:
| 品种甲 | 403 | 397 | 390 | 404 | 388 | 400 | 412 | 406 |
| 品种乙 | 419 | 403 | 412 | 418 | 408 | 423 | 400 | 413 |
为了解某市的交通状况,现对其6条道路进行评估,得分分别为:5,6,7,8,9,10.规定评估的平均得分与全市的总体交通状况等级如下表:
| 评估的平均得分 | 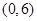 | 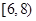 | 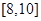 |
| 全市的总体交通状况等级 | 不合格 | 合格 | 优秀 |
(2)用简单随机抽样方法从这
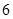 条道路中抽取
条道路中抽取 条,它们的得分组成一个样本,求该样本的平均数与总体的平均数之差的绝对值不超过
条,它们的得分组成一个样本,求该样本的平均数与总体的平均数之差的绝对值不超过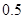 的概率.
的概率. 近年空气质量逐步恶化,雾霾天气现象出现增多,大气污染危害加重.大气污染可引起心悸.呼吸困难等心肺疾病.为了解某市心肺疾病是否与性别有关,在某医院随机的对入院50人进行了问卷调查得到了如下的列联表:
| | 患心肺疾病 | 不患心肺疾病 | 合计 |
| 男 | | 5 | |
| 女 | 10 | | |
| 合计 | | | 50 |
 .
.(1)请将上面的列联表补充完整;
(2)是否有99.5%的把握认为患心肺疾病与性别有关?说明你的理由;
(3)已知在患心肺疾病的10位女性中,有3位又患胃病.现在从患心肺疾病的10位女性中,选出3名进行其他方面的排查,记选出患胃病的女性人数为
 ,求
,求 的分布列,数学期望以及方差.下面的临界值表供参考:
的分布列,数学期望以及方差.下面的临界值表供参考: | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
 ,其中
,其中 )
) 已知离散型随机变量ξ1的概率分布为
| ξ1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| P |  |  |  |  |  |  |  |
| ξ2 | 3.7 | 3.8 | 3.9 | 4 | 4.1 | 4.2 | 4.3 |
| P |  |  |  |  |  |  |  |
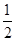 ,乙、丙应聘成功的概率均为
,乙、丙应聘成功的概率均为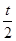 ,(0<t<2),且三个人是否应聘成功是相互独立的.
,(0<t<2),且三个人是否应聘成功是相互独立的. ,若当且仅当为
,若当且仅当为 ,且各次投篮的结果互不影响.甲同学决定投5次,乙同学决定投中1次就停止,否则就继续投下去,但投篮次数不超过5次.
,且各次投篮的结果互不影响.甲同学决定投5次,乙同学决定投中1次就停止,否则就继续投下去,但投篮次数不超过5次. 的分布列和数学期望.
的分布列和数学期望. ,求概率P
,求概率P .
. 的概率.
的概率.