题目内容
8.已知函数f(x)=$\left\{\begin{array}{l}{{2}^{x}-1,0≤x<1}\\{f(x-1),x≥1}\end{array}\right.$,g(x)=k(x+1),若方程f(x)-g(x)=0有四个不同实数根,则k的取值范围为[$\frac{1}{6}$,$\frac{1}{5}$).分析 直线g(x)=k(x+1)恒过定点A(-1,0),则方程f(x)-g(x)=0有四个不同实数根可转化为函数y=f(x)与y=g(x)有且只有四个交点,作出函数f(x)的图象,从图象中得到实数k的取值范围.
解答 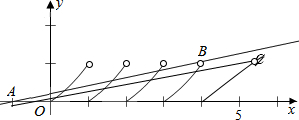 ,解:直线g(x)=k(x+1)恒过定点A(-1,0),
,解:直线g(x)=k(x+1)恒过定点A(-1,0),
则方程f(x)-g(x)=0有四个不同实数根,
可转化为函数y=f(x)与y=g(x)有且只有四个交点,
作出函数f(x)=$\left\{\begin{array}{l}{{2}^{x}-1,0≤x<1}\\{f(x-1),x≥1}\end{array}\right.$
的图象如右图,
由图象可得直线在直线AB和AC之间有4个交点,
由A(-1,0),B(4,1)可得直线AB的斜率为$\frac{1-0}{4-(-1)}$=$\frac{1}{5}$,
由A(-1,0),C(5,1)可得AC的斜率为$\frac{1-0}{5-(-1)}$=$\frac{1}{6}$,
即有k的范围是[$\frac{1}{6}$,$\frac{1}{5}$).
故答案为:[$\frac{1}{6}$,$\frac{1}{5}$).
点评 本题考查了方程的解与函数的零点之间的关系,同时考查了学生的作图能力及数形结合的思想,属于中档题.

练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案
相关题目
19.设函数f(x)=x2+(a-2)x-1在区间[2,+∞)上是增函数,则实数a的最小值为( )
| A. | -2 | B. | -1 | C. | 1 | D. | 2 |
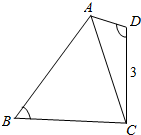 如图所示,在四边形ABCD中,∠D=2∠B,且AD=1,CD=3,cos∠B=$\frac{\sqrt{3}}{3}$
如图所示,在四边形ABCD中,∠D=2∠B,且AD=1,CD=3,cos∠B=$\frac{\sqrt{3}}{3}$