题目内容
16.设函数f(x)=asin2x+bsinx+c,对x∈[0,2π]都有|f(x)|≤1.(1)证明:|c|≤1;
(2)证明:对一切x∈[0,2π],都有|2asinx+b|≤4.
分析 (1)由题意可得|f(0)|≤1,由此可得|c|≤1成立.
(2)令t=sinx,则f(x)=g(t)=a•t2+bt+c,可得g(1)=a+b+c,g(-1)=a-b+c,g(0)=c,求得a、b、c的解析式.根据题意|g(1)|≤1,g(-1)|≤1,|g(0)|≤1.根据|2asinx+b|=|2at+b|=|$\frac{3}{2}$g(1)+$\frac{1}{2}$g(-1)-2g(0)|,分类讨论证得它小于或等于4.
解答 解:(1)证明:由于函数f(x)=asin2x+bsinx+c,对x∈[0,2π]都有|f(x)|≤1.
故有|f(0)|≤1,即|c|≤1.
(2)令t=sinx,则t∈[-1,1],∴f(x)=g(t)=a•t2+bt+c,
可得g(1)=a+b+c,g(-1)=a-b+c,g(0)=c.
求得a=$\frac{g(-1)+g(1)}{2}$-g(0),b=$\frac{g(1)-g(-1)}{2}$,c=g(0).
根据题意|g(1)|≤1,g(-1)|≤1,|g(0)|≤1.
当a≠0时,|2asinx+b|=|2at+b|=|$\frac{3}{2}$g(1)+$\frac{1}{2}$g(-1)-2g(0)|
≤|$\frac{3}{2}$g(1)|+|$\frac{g(-1)}{2}$|+|2g(0)|≤$\frac{3}{2}$+$\frac{1}{2}$+2=4,
即|2asinx+b|≤4成立.
当a=0时,|2asinx+b|=|b|=|$\frac{1}{2}$g(1)-$\frac{1}{2}$g(-1)|≤|$\frac{1}{2}$g(1)|+|$\frac{1}{2}$g(-1)|≤1,
故此时|2asinx+b|≤4成立.
综上可得,对一切x∈[0,2π],都有|2asinx+b|≤4成立.
点评 本题主要考查带有绝对值的函数,绝对值三角不等式的应用,体现了转化、分类讨论的数学思想,属于中档题.

 智能训练练测考系列答案
智能训练练测考系列答案| A. | $\frac{3\sqrt{6}}{2}$ | B. | $\sqrt{6}$ | C. | 3$\sqrt{2}$ | D. | $\frac{3\sqrt{2}}{2}$ |
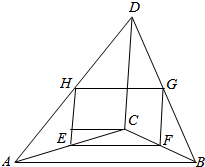 设空间四边形ABCD,E,F,G,H分别是AC,BC,DB,DA的中点,若AB=12$\sqrt{2}$,CD=4$\sqrt{2}$,且四边形EFGH的面积为12$\sqrt{3}$,求AB和CD所成的角.
设空间四边形ABCD,E,F,G,H分别是AC,BC,DB,DA的中点,若AB=12$\sqrt{2}$,CD=4$\sqrt{2}$,且四边形EFGH的面积为12$\sqrt{3}$,求AB和CD所成的角.