题目内容
【题目】已知正三棱锥![]() 每个顶点都在球
每个顶点都在球![]() 的球面上,球心
的球面上,球心![]() 在正三棱锥的内部.球的半径为
在正三棱锥的内部.球的半径为![]() ,且
,且![]() .若过
.若过![]() 作球
作球![]() 的截面,所得圆周长的最大值是
的截面,所得圆周长的最大值是![]() ,则该三棱锥的侧面积为_______.
,则该三棱锥的侧面积为_______.
【答案】![]()
【解析】
依题意,该球的大圆的周长为8π,可得R=4, BC=6.设底面BCD的中心为E,连接BE并延长交CD于F,求得BE,EF,在三角形OBE中应用勾股定理得到OE.可得三棱锥的高AE=AO+OE.所以由勾股定理得到三棱锥的斜高AF .求侧面积即可.
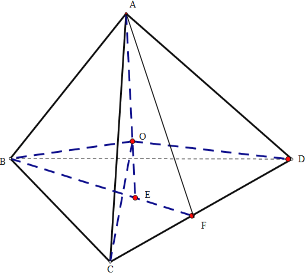
依题意,该球的大圆的周长为8π,所以2πR=8π,得R=4,
如图,正三棱锥A﹣BCD中,设底面三角形BCD的中心为E,则AE⊥平面BCD,
设F为CD的中点,连接BF,AF,则E是BF的三等分点,且AF是三棱锥的侧面ACD的斜高.
根据正三棱锥的对称性,球心O在AE上.
所以BC![]() 6.
6.
则BE![]() 2
2![]() .EF
.EF![]() ,
,
又因为三角形OBE为直角三角形,所以OE![]() 2.
2.
所以三棱锥的高AE=AO+OE=4+2=6.
所以三棱锥的斜高AF![]() .
.
该三棱锥的侧面积为S侧=3![]() 3
3![]() 9
9![]() .
.
故填:![]() .
.

练习册系列答案
相关题目