题目内容
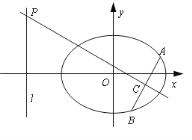
【题目】如图,四边形![]() 为梯形,
为梯形, ![]() ,
, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 为
为![]() 中点.
中点.
(1)求证:平面![]() 平面
平面![]() ;
;
(2)线段![]() 上是否存在一点
上是否存在一点![]() ,使
,使![]() 平面
平面![]() ?若有,请找出具体位置,并进行证明:若无,请分析说明理由.
?若有,请找出具体位置,并进行证明:若无,请分析说明理由.

【答案】(1)证明见解析;(2)当点![]() 位于
位于![]() 三分之一分点(靠近
三分之一分点(靠近![]() 点)时,
点)时, ![]() 平面
平面![]()
【解析】试题分析:(1)证明平面垂直于平面,需要证明一个平面经过另一个平面的一条垂线,根据题意,只需证明; ![]() 平面
平面![]() 即可,只需证明
即可,只需证明![]() 和
和![]() 即可,显然易证;(2)若
即可,显然易证;(2)若![]() 平面
平面![]() ,需要只需要连结
,需要只需要连结![]() 交于
交于![]() 点,根据题意
点,根据题意![]() ,所以
,所以![]() 相似于
相似于![]() ,所以又因为
,所以又因为![]() ,所以
,所以![]() ,从而在
,从而在![]() 中,
中, ![]() ,而
,而![]() ,当点
,当点![]() 位于
位于![]() 三分之一分点(靠近
三分之一分点(靠近![]() 点)时,
点)时, ![]() 平面
平面![]() .
.
试题解析:(1)连结![]()
![]()
![]()
所以![]()
![]() 为
为![]() 中点
中点
所以![]()
又因为![]() 平面
平面![]() , 所以
, 所以![]()
……………4分
所以![]() 平面
平面![]()
因为![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]()
(2)当点![]() 位于
位于![]() 三分之一分点(靠近
三分之一分点(靠近![]() 点)时,
点)时, ![]() 平面
平面![]()
连结![]() 交于
交于![]() 点
点
![]() ,所以
,所以![]() 相似于
相似于![]()
又因为![]() ,所以
,所以![]()
从而在![]() 中,
中, ![]()
而![]()
所以![]()
而![]() 平面
平面![]()
![]() 平面
平面![]()
所以![]() 平面
平面![]()

练习册系列答案
相关题目
【题目】某市对贫困家庭自主创业给予小额贷款补贴,每户贷款额为![]() 万元,贷款期限有
万元,贷款期限有![]() 个月、
个月、![]() 个月、
个月、![]() 个月、
个月、![]() 个月、
个月、![]() 个月五种,这五种贷款期限政府分别需要补助
个月五种,这五种贷款期限政府分别需要补助![]() 元、
元、![]() 元、
元、![]() 元、
元、![]() 元、
元、![]() 元,从
元,从![]() 年享受此项政策的困难户中抽取了
年享受此项政策的困难户中抽取了![]() 户进行了调查统计,选取贷款期限的频数如下表:
户进行了调查统计,选取贷款期限的频数如下表:
贷款期限 |
|
|
|
|
|
频数 |
|
|
|
|
|
以商标各种贷款期限的频率作为![]() 年贫困家庭选择各种贷款期限的概率.
年贫困家庭选择各种贷款期限的概率.
(1)某小区![]() 年共有
年共有![]() 户准备享受此项政策,计算其中恰有两户选择贷款期限为
户准备享受此项政策,计算其中恰有两户选择贷款期限为![]() 个月的概率;
个月的概率;
(2)设给享受此项政策的某困难户补贴为![]() 元,写出
元,写出![]() 的分布列,若预计
的分布列,若预计![]() 年全市有
年全市有![]() 万户享受此项政策,估计
万户享受此项政策,估计![]() 年该市共要补贴多少万元.
年该市共要补贴多少万元.