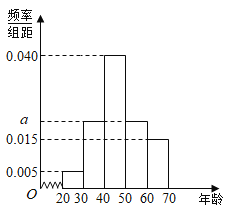
题目内容
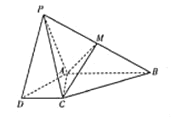
【题目】如图，在多面体
中，四边形
是矩形，
，
，平面
平面．
（1）若
点是
的中点，求证：
平面
；
（2）求证：平面
平面
；
（3）若
，求直线
与平面
成角的正弦值．
【答案】（1）见解析；（2）见解析；（3）
【解析】
（1）点
是
中点，易证四边形
是平行四边形，从而
，利用线面平行的判断定理即可得到
面
；（2）依题意，可证
平面
，利用面面垂直的判断定理即可证得面
面
；（3）首先证明
面
，即
为直线
与平面成角，求出即可求出线面角的正弦值.
（1）如图，
∵点是中点，
，
，
∴
且
，
∴四边形是平行四边形，∴，
又
面，
面，
∴面．
（2）∵平面
平面
，平面
平面
，
，
∴平面，
又
平面，∴面面.
（3）在直角梯形
中，
，
，
∴
且
，
∴
，
由（2）知平面，
，
∴
平面，∴
，
又∵
，∴面，即为直线与平面成角，
又∵
，∴
，
∴直线与平面成角的正弦值为.
练习册系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
