题目内容
【题目】已知函数![]() ,
,![]() .
.
(1)若![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
(2)设函数![]() 的极大值为
的极大值为![]() ,极小值为
,极小值为![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ; (2)
; (2)![]() .
.
【解析】
(1)根据题意转化为![]() 的最小值小于等于9,二次函数根据轴与区间的关系进行分类讨论,得到答案.(2)利用导数求出
的最小值小于等于9,二次函数根据轴与区间的关系进行分类讨论,得到答案.(2)利用导数求出![]() 的极小值
的极小值![]() 和极大值
和极大值![]() ,并且得到
,并且得到![]()
![]() 的关系,以及
的关系,以及![]() 与
与![]()
![]() 的关系,表示出
的关系,表示出![]() 消去
消去![]() ,然后令
,然后令![]() ,将
,将![]() 转化成关于
转化成关于![]() 的函数,注意
的函数,注意![]() 的取值范围,从而求出
的取值范围,从而求出![]() 的范围.
的范围.
(1)因为![]() ,
,
所以函数![]() 的最小值小于等于9.
的最小值小于等于9.
(i)函数![]() 的对称轴为
的对称轴为![]() ,当
,当![]() ,即
,即![]() 时,
时,
由![]() ,得
,得![]() ,
,
因为![]() ,所以
,所以![]() ;
;
(ii)当![]() ,即
,即![]() 时,
时,
由![]() ,得
,得![]() .
.
综上,实数![]() 的取值范围为
的取值范围为![]() .
.
(2)因为![]() ,所以
,所以![]() .
.
设![]() ,因为
,因为![]() ,
,
所以函数![]() 有两个不同的零点,不妨设为
有两个不同的零点,不妨设为![]() ,
,![]() ,且
,且![]() ,
,
则![]() ,
,![]() .
.
当![]() 时,
时,![]() ,函数
,函数![]() 为单调递减函数;
为单调递减函数;
当![]() 时,
时,![]() ,函数
,函数![]() 为单调递增函数;
为单调递增函数;
当![]() 时,
时,![]() ,函数
,函数![]() 为单调递减函数.
为单调递减函数.
所以当![]() 时,函数
时,函数![]() 取得极小值,当
取得极小值,当![]() 时,函数
时,函数![]() 取得极大值,
取得极大值,
所以![]() ,
,
又![]() ,
,![]() ,所以
,所以![]() .
.
将![]() 代入
代入![]() ,得
,得![]() ,
,
设![]() ,则
,则![]()
![]() ,
,
所以![]() .
.
设![]() ,
,![]() ,则
,则![]() ,
,
所以函数![]() 在
在![]() 上为单调减函数,
上为单调减函数,
从而![]() ,
,
又![]() ,当
,当![]() 时,
时,![]() ,所以
,所以![]() ,
,
即![]() .
.
故![]() 的取值范围为
的取值范围为![]() .
.

 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案【题目】某学生为了测试煤气灶烧水如何节省煤气的问题设计了一个实验,并获得了煤气开关旋钮旋转的弧度数![]() 与烧开一壶水所用时间
与烧开一壶水所用时间![]() 的一组数据,且作了一定的数据处理(如下表),得到了散点图(如下图).
的一组数据,且作了一定的数据处理(如下表),得到了散点图(如下图).
|
|
|
|
|
|
|
|
|
|
|
|
|
|
表中![]() ,
,![]() .
.

(1)根据散点图判断,![]() 与
与![]() 哪一个更适宜作烧水时间
哪一个更适宜作烧水时间![]() 关于开关旋钮旋转的弧度数
关于开关旋钮旋转的弧度数![]() 的回归方程类型?(不必说明理由)
的回归方程类型?(不必说明理由)
(2)根据判断结果和表中数据,建立![]() 关于
关于![]() 的回归方程;
的回归方程;
(3)若单位时间内煤气输出量![]() 与旋转的弧度数
与旋转的弧度数![]() 成正比,那么,利用第(2)问求得的回归方程知
成正比,那么,利用第(2)问求得的回归方程知![]() 为多少时,烧开一壶水最省煤气?
为多少时,烧开一壶水最省煤气?
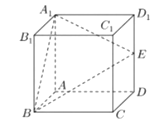
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘法估计值分别为
的斜率和截距的最小二乘法估计值分别为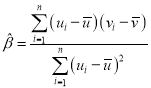 ,
,![]()
【题目】某品牌餐饮公司准备在10个规模相当的地区开设加盟店,为合理安排各地区加盟店的个数,先在其中5个地区试点,得到试点地区加盟店个数分别为1,2,3,4,5时,单店日平均营业额![]() (万元)的数据如下:
(万元)的数据如下:
加盟店个数 | 1 | 2 | 3 | 4 | 5 |
单店日平均营业额 | 10.9 | 10.2 | 9 | 7.8 | 7.1 |
(1)求单店日平均营业额![]() (万元)与所在地区加盟店个数
(万元)与所在地区加盟店个数![]() (个)的线性回归方程;
(个)的线性回归方程;
(2)根据试点调研结果,为保证规模和效益,在其他5个地区,该公司要求同一地区所有加盟店的日平均营业额预计值总和不低于35万元,求一个地区开设加盟店个数![]() 的所有可能取值;
的所有可能取值;
(3)小赵与小王都准备加入该公司的加盟店,根据公司规定,他们只能分别从其他五个地区(加盟店都不少于2个)中随机选一个地区加入,求他们选取的地区相同的概率.
(参考数据及公式:![]() ,
,![]() ,线性回归方程
,线性回归方程![]() ,其中
,其中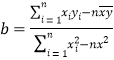 ,
,![]() .)
.)