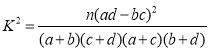题目内容
【题目】已知函数![]() .
.
(1)求函数![]() 的值域;
的值域;
(2)试问:函数![]() 的图象上是否存在关于坐标原点对称的点,若存在,求出这些点的坐标;若不存在,说明理由;
的图象上是否存在关于坐标原点对称的点,若存在,求出这些点的坐标;若不存在,说明理由;
(3)若方程![]() 的三个实数根
的三个实数根![]() 、
、![]() 、
、![]() 满足:
满足:![]() <
<![]() <
<![]() ,且
,且![]() ,求实数a的值.
,求实数a的值.
【答案】(1)![]() ;(2)存在,分别是
;(2)存在,分别是![]() ,
,![]() ;(3)
;(3)![]() .
.
【解析】
(1)分别求出函数在每段上的值域,最后求出整个函数的值域即可.
(2)假设存在这样的点,不妨设![]() ,可求它的关于原点的对称点坐标,再代入函数解析式中,能求出
,可求它的关于原点的对称点坐标,再代入函数解析式中,能求出![]() 说明存在性,求不出
说明存在性,求不出![]() 则说明不存在这样的点;
则说明不存在这样的点;
(3)判断![]() 之间的大小关系,然后分类化简方程,求出三个实数根
之间的大小关系,然后分类化简方程,求出三个实数根![]() 、
、![]() 、
、![]() ,再根据
,再根据![]() ,求出实数a的值.
,求出实数a的值.
(1)当![]() 时,
时, ![]()
当![]() 时,
时, ![]() ,因此函数的值域为
,因此函数的值域为![]() ;
;
(2) 假设存在这样的点,不妨设![]() ,它关于原点的对称点坐标为:
,它关于原点的对称点坐标为:
![]() ,由题意可知它也在函数图象上,因此有
,由题意可知它也在函数图象上,因此有
![]() (舍去),
(舍去),
因此存在这样两个点,坐标分别为![]() 和
和![]() ;
;
(3)由(1)可知:当![]() 时,
时, ![]() ,显然此时,
,显然此时, ![]() ,
,
当![]() 时,若
时,若![]() 时,解得
时,解得![]() ,若
,若![]() 时,解得
时,解得
![]() .
.
因此当![]() 时,
时, ![]() ,此时方程化简为:
,此时方程化简为:![]()
解得![]() ,因此有
,因此有![]() .
.
当![]() 时,
时, ![]() ,此时方程化简为:
,此时方程化简为:![]() ,解得
,解得
![]() ,要想方程有三个不同的根,则必有
,要想方程有三个不同的根,则必有![]() ,此时
,此时
![]() 成立,因此有
成立,因此有![]() ,
,
又因为![]() ,
,
所以![]() ,解得
,解得![]() (舍去),
(舍去), ![]() .
.
![]() ,因此
,因此![]() .
.

【题目】为了调查某生产线上质量监督员甲是否在现场对产品质量好坏有无影响,现统计数据如下:质量监督员甲在现场时,1 000件产品中合格品有990件,次品有10件,甲不在现场时,500件产品中有合格品490件,次品有10件.
(1)补充下面列联表,并初步判断甲在不在现场与产品质量是否有关:
合格品数/件 | 次品数/件 | 总数/件 | |
甲在现场 | 990 | ||
甲不在现场 | 10 | ||
总数/件 |
(2)用独立性检验的方法判断能否在犯错误的概率不超过0.15的前提下认为“甲在不在现场与产品质量有关”?
P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
K | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |