题目内容
【题目】若F1 , F2是椭圆C: ![]() +
+ ![]() =1(0<m<9)的两个焦点,椭圆上存在一点P,满足以椭圆短轴为直径的圆与线段PF1相切于该线段的中点M. (Ⅰ)求椭圆C的方程;
=1(0<m<9)的两个焦点,椭圆上存在一点P,满足以椭圆短轴为直径的圆与线段PF1相切于该线段的中点M. (Ⅰ)求椭圆C的方程;
(Ⅱ)过点(0, ![]() )的直线l与椭圆C交于两点A、B,线段AB的中垂线l1交x轴于点N,R是线段AN的中点,求直线l1与直线BR的交点E的轨迹方程.
)的直线l与椭圆C交于两点A、B,线段AB的中垂线l1交x轴于点N,R是线段AN的中点,求直线l1与直线BR的交点E的轨迹方程.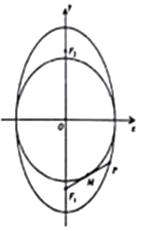
【答案】解:(Ⅰ)∵0<m<9,∴a=3,b= ![]() ,不妨设椭圆的下焦点F1 , 设线段PF1的中点为:M; 由题意,OM⊥PF1 , 又OM=b,OM是△PF1F2的中位线,
,不妨设椭圆的下焦点F1 , 设线段PF1的中点为:M; 由题意,OM⊥PF1 , 又OM=b,OM是△PF1F2的中位线,
∴|PF2|=2b,
由椭圆定义,|PF1|=2a﹣2b=6﹣2b.∴ ![]() =3﹣b,
=3﹣b,
在Rt△OMF1中: ![]() ,
,
∴c2=b2+(3﹣b)2 , 又c2=a2﹣b2=9﹣b2 . ,
∴b2+(3﹣b)2=9﹣b2交点b=0(舍去)或b=2,∴m=b2=4.
∴椭圆C的方程: ![]() +
+ ![]() =1.
=1.
(Ⅱ)由(Ⅰ)椭圆C的方程: ![]() +
+ ![]() =1.
=1.
上焦点坐标(0, ![]() ).直线l的斜率k必存在.
).直线l的斜率k必存在.
设A(x1 , y1)B(x2 , y2),弦AB的中点Q(x0 , y0),
由 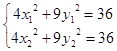 ,可得4(y1+y2)(y1﹣y2)=﹣9(x1+x2)(x1﹣x2),
,可得4(y1+y2)(y1﹣y2)=﹣9(x1+x2)(x1﹣x2),
∴k= ![]() =﹣
=﹣ ![]() =﹣
=﹣ ![]() (y0≠0)
(y0≠0)
①当x0≠0时,k=kAB= ![]() ∴k=-
∴k=- ![]() =
= ![]() 9x02+4y02﹣4
9x02+4y02﹣4 ![]() y0=0,
y0=0,
又l1:y﹣y0= ![]() ,∴N(
,∴N( ![]() ),
),
连结BN,则E为△ABN的重心,设E(x,y),
则 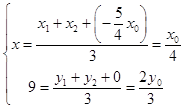 ,
,
∴ 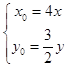 代入9x02+4y02﹣4
代入9x02+4y02﹣4 ![]() y0=0可得:48x2+3y2﹣2
y0=0可得:48x2+3y2﹣2 ![]() ,(y≠0).
,(y≠0).
②当x0=0时,l:y= ![]() ,N(0,0),E(0,
,N(0,0),E(0, ![]() )也适合上式,
)也适合上式,
综上所述,点E的轨迹方程为:48x2+3y2﹣2 ![]() ,(y≠0).
,(y≠0).
【解析】(Ⅰ)求出a=3,b= ![]() ,设椭圆的下焦点F1 , 设线段PF1的中点为:M;由题意,OM⊥PF1 , 又OM=b,OM是△PF1F2的中位线,由椭圆定义,在Rt△OMF1中的勾股定理,求出b=2,得到m.然后求解椭圆C的方程. (Ⅱ)上焦点坐标(0,
,设椭圆的下焦点F1 , 设线段PF1的中点为:M;由题意,OM⊥PF1 , 又OM=b,OM是△PF1F2的中位线,由椭圆定义,在Rt△OMF1中的勾股定理,求出b=2,得到m.然后求解椭圆C的方程. (Ⅱ)上焦点坐标(0, ![]() ).直线l的斜率k必存在.设A(x1 , y1)B(x2 , y2),弦AB的中点Q(x0 , y0),利用平方差法得到AB的斜率,通过①当x0≠0时,k=kAB=
).直线l的斜率k必存在.设A(x1 , y1)B(x2 , y2),弦AB的中点Q(x0 , y0),利用平方差法得到AB的斜率,通过①当x0≠0时,k=kAB= ![]() ,推出9x02+4y02﹣4
,推出9x02+4y02﹣4 ![]() y0=0,连结BN,则E为△ABN的重心,设E(x,y),利用重心坐标公式,推出
y0=0,连结BN,则E为△ABN的重心,设E(x,y),利用重心坐标公式,推出 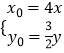 代入9x02+4y02﹣4
代入9x02+4y02﹣4 ![]() y0=0轨迹方程②当x0=0时,验证即可.
y0=0轨迹方程②当x0=0时,验证即可.

 阅读快车系列答案
阅读快车系列答案【题目】2016年微信用户数量统计显示,微信注册用户数量已经突破9.27亿.微信用户平均年龄只有26岁,97.7%的用户在50岁以下,86.2%的用户在18﹣36岁之间.为调查大学生这个微信用户群体中每人拥有微信群的数量,现从北京市大学生中随机抽取100位同学进行了抽样调查,结果如下:
微信群数量 | 频数 | 频率 |
0至5个 | 0 | 0 |
6至10个 | 30 | 0.3 |
11至15个 | 30 | 0.3 |
16至20个 | a | c |
20个以上 | 5 | b |
合计 | 100 | 1 |
(Ⅰ)求a,b,c的值;
(Ⅱ)若从这100位同学中随机抽取2人,求这2人中恰有1人微信群个数超过15个的概率;
(Ⅲ)以这100个人的样本数据估计北京市的总体数据且以频率估计概率,若从全市大学生中随机抽取3人,记X表示抽到的是微信群个数超过15个的人数,求X的分布列和数学期望EX.