题目内容
【题目】我国唐代诗人王维诗云：“明月松间照，清泉石上流”，这里明月和清泉，都是自然景物，没有变，形容词“明”对“清”，名词“月”对“泉”，词性不变，其余各词均如此．变化中的不变性质，在文学和数学中都广泛存在．比如我们利用几何画板软件作出抛物线C：x2=y的图象（如图），过交点F作直线l交C于A、B两点，过A、B分别作C的切线，两切线交于点P，过点P作x轴的垂线交C于点N，拖动点B在C上运动，会发现 
是一个定值，该定值是 ． 
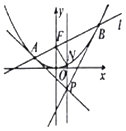
【答案】1
【解析】解：线段AB是过抛物线x2=y焦点F的弦，过A，B两点分别作此抛物线的切线，两切线相交于N点．N点在抛物线的准线上．下面证明
证明：由抛物线x2=y，得其焦点坐标为F（0， 
）．
设A（x1 ， x12），B（x2 ， x22），
直线l：y=kx+ 代入抛物线x2=y得：x2﹣kx﹣ =0．
∴x1x2=﹣ …①．
又抛物线方程为：y=x2 ，
求导得y′=2x，
∴抛物线过点A的切线的斜率为2x1 ， 切线方程为y﹣x12=2x1（x﹣x1）…②
抛物线过点B的切线的斜率为2x2 ， 切线方程为yx22﹣=2x2（x﹣x2）…③
由①②③得：y=﹣ ．
∴P的轨迹方程是y=﹣ ，即N在抛物线的准线上；
根据抛物线的定义知：NF=NP，∴ 
是一个定值1．
所以答案是：1
练习册系列答案
相关题目
