题目内容
【题目】设数列![]() 的前
的前![]() 项和为
项和为![]() ,若
,若![]() ,则称
,则称![]() 是“
是“![]() 数列”.
数列”.
(1)若![]() 是“
是“![]() 数列”,且
数列”,且![]() ,
,![]() ,
,![]() ,
,![]() ,求
,求![]() 的取值范围;
的取值范围;
(2)若![]() 是等差数列,首项为
是等差数列,首项为![]() ,公差为
,公差为![]() ,且
,且![]() ,判断
,判断![]() 是否为“
是否为“![]() 数列”;
数列”;
(3)设数列![]() 是等比数列,公比为
是等比数列,公比为![]() ,若数列
,若数列![]() 与
与![]() 都是“
都是“![]() 数列”,求
数列”,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ; (2)见解析; (3)
; (2)见解析; (3)![]() .
.
【解析】
(1)根据数列的新定义,列出不等式组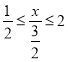 且
且![]() ,,即可求解;
,,即可求解;
(2)由等差数列![]() ,得到
,得到![]() ,进而得出
,进而得出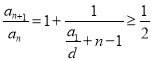 ,再由
,再由![]() 的单调性,得到
的单调性,得到![]() ,即可得到结论;
,即可得到结论;
(3)设等比数列![]() 的公比为
的公比为![]() ,分
,分![]() 和
和![]() 时,结合数列的新定义,即可作差判定.
时,结合数列的新定义,即可作差判定.
(1)由题意,数列![]() 满足
满足![]() ,称
,称![]() 是“
是“![]() 数列”,
数列”,
又由![]() ,
,![]() ,
,![]() ,
,![]() ,可得
,可得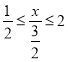 且
且![]() ,
,
解得![]() ,即
,即![]() 的取值范围是
的取值范围是![]() .
.
(2)由题意,数列![]() 的通项公式为
的通项公式为![]() ,
,
则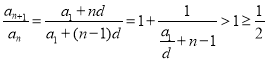 ,
,
又由![]() ,可得数列
,可得数列![]() 随着
随着![]() 的增大而减小,
的增大而减小,
所以当![]() 时,
时,![]() 取得最大值,所以
取得最大值,所以![]() ,
,
所以数列![]() 是“
是“![]() 数列”.
数列”.
(3)由题意得,等比数列![]() 的公比为
的公比为![]() ,
,
由数列![]() 是“G的数列”,可得
是“G的数列”,可得![]() ,即
,即![]() ,
,
①当![]() 时,所以
时,所以![]() ,则
,则![]() ,符合题意,
,符合题意,
②当![]() 时,则
时,则![]() ,则
,则![]() ,
,
因为数列![]() 是“G的数列”,所以
是“G的数列”,所以![]() 对
对![]() 恒成立,
恒成立,
(i)当![]() 时,
时,![]() ,
,
即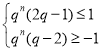 对
对![]() 恒成立,
恒成立,
因为![]() ,
,
所以![]() ,
,
所以当![]() 时,
时,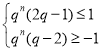 对
对![]() 恒成立;
恒成立;
(ii)当![]() 时,
时,![]() ,
,
即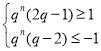 对
对![]() 恒成立,
恒成立,
因为![]() ,
,
所以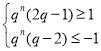 ,解得
,解得![]() ,
,
又![]() ,所以不存在
,所以不存在![]() 满足题意,
满足题意,
综上可得,数列![]() 的公比
的公比![]() 的取值范围是
的取值范围是![]() .
.

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
【题目】唐三彩,中国古代陶瓷烧制工艺的珍品,它吸取了中国国画、雕塑等工艺美术的特点,在中国文化中占有重要的历史地位,在中国的陶瓷史上留下了浓墨重彩的一笔.唐三彩的生产至今已有![]() 多年的历史,对唐三彩的复制和仿制工艺,至今也有百余年的历史.某陶瓷厂在生产过程中,对仿制的
多年的历史,对唐三彩的复制和仿制工艺,至今也有百余年的历史.某陶瓷厂在生产过程中,对仿制的![]() 件工艺品测得重量(单位:
件工艺品测得重量(单位:![]() )数据如下表:
)数据如下表:
分组 | 频数 | 频率 |
|
|
|
|
| |
|
| |
|
|
|
|
| |
|
| |
合计 |
|
(1)求出频率分布表中实数![]() ,
,![]() 的值;
的值;
(2)若从仿制的![]() 件工艺品重量范围在
件工艺品重量范围在![]() 的工艺品中随机抽选
的工艺品中随机抽选![]() 件,求被抽选
件,求被抽选![]() 件工艺品重量均在范围
件工艺品重量均在范围![]() 中的概率.
中的概率.