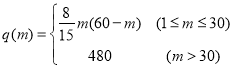题目内容
【题目】在数列![]() 中,
中,![]() ,其中
,其中![]() .
.
(1)若![]() 依次成公差不为0的等差数列,求m;
依次成公差不为0的等差数列,求m;
(2)证明:“![]() ”是“
”是“![]() 恒成立”的充要条件;
恒成立”的充要条件;
(3)若![]() ,求证:存在
,求证:存在![]() ,使得
,使得![]() .
.
【答案】(1)![]() ;(2)证明略;(3)证明略。
;(2)证明略;(3)证明略。
【解析】
(1)由![]() 得出
得出![]() ,再因为
,再因为 ![]() 依次成公差不为0的等差数列,可得
依次成公差不为0的等差数列,可得![]() ,可求得
,可求得![]() 的值;
的值;
(2)由![]() ,得出
,得出![]() ,再由
,再由![]() ,可得
,可得![]() ,由此可证充分性;再
,由此可证充分性;再 ![]() 对
对![]() 恒成立,可得
恒成立,可得![]() 对
对![]() 恒成立,可得出
恒成立,可得出![]() 可证其必要性,可得证;
可证其必要性,可得证;
(3)由![]() ,
,![]()
![]()
![]()
![]() ,将上述不等式相加得
,将上述不等式相加得 ![]() ,可取正整数
,可取正整数![]() ,可得证.
,可得证.
(1)由![]() 得,
得,![]() ,
,![]() ,
,![]() ,
,
因为![]() 依次成公差不为0的等差数列,所以
依次成公差不为0的等差数列,所以![]() ,
,
即![]() ,解得
,解得![]() (
(![]() 舍去),经检验,此时
舍去),经检验,此时![]() 的公差不为
的公差不为![]() ,
,
所以![]() ;
;
(2)因为![]() ,因为
,因为![]() ,所以
,所以![]() ,因为
,因为![]() ,所以
,所以![]() ,
,
所以“![]() ”是“
”是“![]() ”恒成立的充分条件;
”恒成立的充分条件;
因为![]() ,
,![]() ,所以
,所以![]() 对
对![]() 恒成立,即
恒成立,即![]() 对
对![]() 恒成立,
恒成立,
而![]() ,所以
,所以![]() ,要使
,要使![]() 对
对![]() 恒成立,则需
恒成立,则需![]() ,
,
所以“![]() ”是“
”是“![]() ”恒成立的必要条件,
”恒成立的必要条件,
所以“![]() ”是“
”是“![]() 恒成立”的充要条件.
恒成立”的充要条件.
(3)因为![]() ,又因为
,又因为![]()
所以令![]() ,
,
![]()
![]()
![]()
![]() ,
,
将上述不等式相加得 ![]() ,所以
,所以 ![]() ,
,
取正整数![]() ,有
,有 ![]() ,
,
所以当![]() ,存在
,存在![]() ,使得
,使得![]() .
.

练习册系列答案
相关题目