题目内容
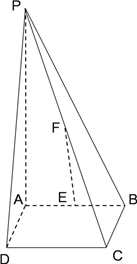
【题目】如图,四棱锥![]() 的底面是边长为
的底面是边长为![]() 的正方形,
的正方形, ![]() 底面
底面![]() ,
, ![]() 分别为
分别为![]() 的中点.
的中点.
(Ⅰ)求证: ![]()
![]() 平面
平面![]() ;
;
(Ⅱ)若![]() ,试问在线段
,试问在线段![]() 上是否存在点
上是否存在点![]() ,使得二面角
,使得二面角 ![]() 的余弦值为
的余弦值为![]() ?若存在,确定点
?若存在,确定点![]() 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.
【答案】(Ⅰ)证明见解析;(Ⅱ)满足条件的![]() 存在,是
存在,是![]() 中点
中点
【解析】试题分析:(1)证明线面平行,一般利用线面平行判定定理,即从线线平行出发给予证明,而线线平行的寻找与论证,往往需要结合平几知识,如本题取PD中点M,利用三角形中位线性质得![]() ,再结合平行四边形性质得四边形EFMA为平行四边形,从而得出EF∥AM,(2)涉及二面角问题,一般利用空间向量进行解决,首先根据题意建立恰当的空间直角坐标系,设立各点坐标,利用方程组求各面的法向量,结合向量数量积求向量夹角,最后根据二面角与向量夹角的关系列等量关系,求出待定参数
,再结合平行四边形性质得四边形EFMA为平行四边形,从而得出EF∥AM,(2)涉及二面角问题,一般利用空间向量进行解决,首先根据题意建立恰当的空间直角坐标系,设立各点坐标,利用方程组求各面的法向量,结合向量数量积求向量夹角,最后根据二面角与向量夹角的关系列等量关系,求出待定参数
试题解析:证明:(Ⅰ)取PD中点M,连接MF、MA,
在△PCD中,F为PC的中点,∴![]() ,
,
正方形ABCD中E为AB中点,∴![]() ,∴
,∴![]() ,
,
故四边形EFMA为平行四边形,∴EF∥AM,
又∵EF平面PAD,AM平面PAD,
∴EF∥平面PAD;
(Ⅱ)结论:满足条件的Q存在,是EF中点.理由如下:
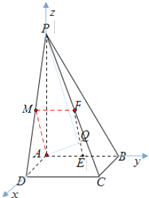
如图:以点A为坐标原点建立空间直角坐标系,
则P(0,0,2),B(0,1,0),C(1,1,0),E(0, ![]() ,0),F(
,0),F(![]() ,
, ![]() ,1),
,1),
由题易知平面PAD的法向量为![]() =(0,1,0),
=(0,1,0),
假设存在Q满足条件:设![]() ,
,
∵![]() ,∴
,∴![]() ,
, ![]() ,λ∈,
,λ∈,
设平面PAQ的法向量为![]() ,
,
由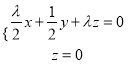 ,可得
,可得![]() ,
,
∴![]() ,
,
由已知: 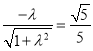 ,解得:
,解得: ![]() ,
,
所以满足条件的Q存在,是EF中点.

练习册系列答案
 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案
相关题目

