题目内容
【题目】已知数列{an}的前n项和Sn＝－
n2＋
n，求数列{|an|}的前n项和Tn.
【答案】
【解析】试题分析：由Sn＝－
n2＋
n可得
，故可得当当n≤34时，an>0；当n≥35时，an<0，分两种情况求数列{|an|}的前n项和Tn
试题解析：
当n≥2时， 
，
an＝Sn－Sn－1＝－3n＋104.
又
时，a1＝S1＝－
×12＋
×1＝101，满足上式，
∴数列{an}的通项公式为an＝－3n＋104(n∈N*)．
由an＝－3n＋104≥0，得n≤34.7.
即当n≤34时，an>0；当n≥35时，an<0
①当n≤34时，
Tn＝|a1|＋|a2|＋…＋|an|
＝a1＋a2＋…＋an
＝Sn＝－n2＋n.
②当n≥35时，
Tn＝|a1|＋|a2|＋…＋|a34|＋|a35|＋…＋|an|
＝(a1＋a2＋…＋a34)－(a35＋a36＋…＋an)
＝2(a1＋a2＋…＋a34)－(a1＋a2＋…＋an)
＝2S34－Sn
＝2
－
＝n2－n＋3502.
综上Tn＝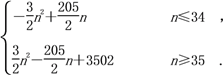
练习册系列答案
相关题目
【题目】某单位附近只有甲、乙两个临时停车场，它们各有
个车位，为了方便市民停车，某互联网停车公司对这两个停车场，在某些固定时刻的剩余停车位进行记录，如下表：
时间 停车场 |
|
|
|
|
|
|
甲停车场 |
|
|
|
|
|
|
乙停车场 |
|
|
|
|
|
|
如果表中某一时刻剩余停车位数低于该停车场总车位数的
，那么当车主驱车抵达单位附近时，该公司将会向车主发出停车场饱和警报.
（1）假设某车主在以上六个时刻抵达单位附近的可能性相同，求他收到甲停车场饱和警报的概率；
（2）从这六个时刻中任选一个时刻,求甲停车场比乙停车场剩余车位数少的概率；
（3）当乙停车场发出饱和警报时，求甲停车场也发出饱和警报的概率.
