题目内容
【题目】在某校组织的“共筑中国梦”竞赛活动中，甲、乙两班各有6名选手参赛，在第一轮笔试环节中，评委将他们的笔试成绩作为样本数据，绘制成如图所示的茎叶图，为了增加结果的神秘感，主持人故意没有给出甲、乙两班最后一位选手的成绩，只是告诉大家，如果某位选手的成绩高于90分（不含90分），则直接“晋级” （Ⅰ）求乙班总分超过甲班的概率
（Ⅱ）主持人最后宣布：甲班第六位选手的得分是90分，乙班第六位选手的得分是97分
①请你从平均分光和方差的角度来分析两个班的选手的情况；
②主持人从甲乙两班所有选手成绩中分别随机抽取2个，记抽取到“晋级”选手的总人数为ξ，求ξ的分布列及数学期望．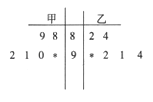
【答案】解：（Ⅰ）甲班前5位选手的总分为88+89+90+91+92=450， 乙班前5位选手的总分为82+84+92+91+94=443，
若乙班总分超过甲班，则甲、乙两班第六位选手的成绩可分别为：
（90，98），（90，99），（91，99），共三个，
∴乙班总分超过甲班的概率为p= 
= 
．
（Ⅱ）①甲班平均分为 
= 
（88+89+90+91+92+90）=90，
乙班平均数为 
= （82+84+92+91+94+97）=90，
甲班方差为S2甲= （22+12+12+22）= 
，
乙班方差为S2乙= （82+62+22+12+42+72）= 
，
两班的平均分相同，但甲班选手的方差小于乙班，
故甲班选手间的实力相当，相差不大，乙班选手间实力悬殊，差距较大．
②ξ的可能取值为0，1，2，3，4，
P（ξ=0）= 
= 
，
P（ξ=1）= 
= 
，
P（ξ=2）= 
= 
，
P（ξ=3）= 
= ，
P（ξ=4）= 
= ，
∴ξ的分布列为：
ξ | 0 | 1 | 2 | 3 | 4 |
P |
|
|
|
|
|
∴E（ξ）= 
=2
【解析】（Ⅰ）先分别求出甲班前5位选手的总分和乙班前5位选手的总分，由此利用列举法能求出乙班总分超过甲班的概率．（Ⅱ）①分别求出甲、乙两班平均分和方差，由此能求出甲班选手间的实力相当，相差不大，乙班选手间实力悬殊，差距较大．②ξ的可能取值为0，1，2，3，4，分别求出相应的概率，由此能求出ξ的分布列和E（ξ）．
【考点精析】本题主要考查了频率分布直方图的相关知识点，需要掌握频率分布表和频率分布直方图，是对相同数据的两种不同表达方式.用紧凑的表格改变数据的排列方式和构成形式，可展示数据的分布情况.通过作图既可以从数据中提取信息，又可以利用图形传递信息才能正确解答此题．
