��Ŀ����
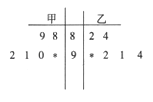
����Ŀ��Ϊ���ﴫͳ�Ļ���ijУ����ʫ�ʴ������������ѡ�Σ����ռ������˽��������������Ǿ��������������£��ٱ�������������⣻�ڱ���ǰ���˴�����Ⱥ�˳��ͨ����ǩ������˫���������⣬ÿ�λش�һ������������ԣ��Լ���1�֣����������Է���1�֣����ȵ� 3 ����ʤ����֪�ס��Ҵ��ÿ����ĸ��ʷֱ�Ϊ ![]() ��
�� ![]() ����ÿ�δ���Ľ���������
����ÿ�δ���Ľ���������
���������ȴ��⣬���3��0��ʤ�ĸ��ʣ�
���������ȴ��⣬�������÷���Ϊ X����X�ķֲ��к���ѧ���� EX��
���𰸡��⣺��I���衰���ȴ��⣬��3��0��ʤ��Ϊ�¼�A��ֻ���Ǵ���3�����������ʱ�Ҵ��2���⣬�״��1���⣮ ��P1= ![]() =
= ![]() ��
��
��II��������ɵã�X�Ŀ���ȡֵΪ0��1��2��3��
�� X=0ʱ�������3�����������ʱ�Ҵ��1���⣬�״��2���⣬��ʱ��3�֣��ҵ�0�֣���P��X=0��= ![]() ����1��
����1�� ![]() ����
���� ![]() =
= ![]() ��
��
��X=1�������4�����������ʱ����һ��3��������״��Ҵ����Ҵ������Ҵ��״��Ҵ���
���ҶԼ��Ҵ���
��P��X=1��=��1�� ![]() ������1��
������1�� ![]() ����
���� ![]() ����1��
����1�� ![]() ��+
��+ ![]() ����1��
����1�� ![]() ������1��
������1�� ![]() ������1��
������1�� ![]() ��+
��+ ![]() ��
�� ![]() ��
�� ![]() ����1��
����1�� ![]() ��=
��= ![]() ��
��
��X=2�����5�α����Ǽ״�ԣ���ʱ����һ��6����������ҶԼ��ҶԼԣ����ҶԼ״��Ҵ��ԣ����Ҵ��״��ҶԼԣ��״��ҶԼ��Ҵ��ԣ��״��Ҵ����ҶԼԣ��״��Ҵ��״��Ҵ��ԣ�
��P��X=2��= ![]() ��4+
��4+ ![]() +
+ ![]() =
= ![]() ��
��
��X=3��P��X=3��=1��P��X=0����P��X=1����P��X=2��=1�� ![]() ��
�� ![]() ��
�� ![]() =
= ![]() ��
��
��ֲ���Ϊ��
X | 0 | 1 | 2 | 3 |
P |
|
|
|
|
E��X��=0+ ![]() +2��
+2�� ![]() +
+ ![]() =
= ![]()
����������I���衰���ȴ��⣬��3��0��ʤ��Ϊ�¼�A��ֻ���Ǵ���3�����������ʱ�Ҵ��2���⣬�״��1���⣮ ���ɵó�����II��������ɵã�X�Ŀ���ȡֵΪ0��1��2��3��
��X=0ʱ�������3�����������ʱ�Ҵ��1���⣬�״��2���⣬��ʱ��3�֣��ҵ�0�֣����ɵó�����X=1�������4�����������ʱ����һ��3��������״��Ҵ����Ҵ������Ҵ��״��Ҵ������ҶԼ��Ҵ�����X=2�����5�α����Ǽ״�ԣ���ʱ����һ��6����������ҶԼ��ҶԼԣ����ҶԼ״��Ҵ��ԣ����Ҵ��״��ҶԼԣ��״��ҶԼ��Ҵ��ԣ��״��Ҵ����ҶԼԣ��״��Ҵ��״��Ҵ��ԣ���X=3��P��X=3��=1��P��X=0����P��X=1����P��X=2����
�����㾫����������Ĺؼ�����������ɢ�������������ֲ��е����֪ʶ���������������Ʒ����������У������������X����ȡ��ֵ�����ǿ���һ������һһ�г����������������������ɢ�������������ɢ����������ķֲ��У�һ���,����ɢ���������X����ȡ��ֵΪx1,x2,.....,xi,......,xn��Xȡÿһ��ֵ xi(i=1,2,......���ĸ���P(��=xi����Pi����Ʊ�Ϊ��ɢ���������X �ĸ��ʷֲ�����Ʒֲ��У�

 �����ߴ���ϵ�д�
�����ߴ���ϵ�д�