题目内容
已知函数 是一次函数,且
是一次函数,且
 成等比数列,设
成等比数列,设 ,(
,(  )
)
(1)求Tn;
(2)设 ,求数列
,求数列 的前n项和
的前n项和 .
.
 是一次函数,且
是一次函数,且
 成等比数列,设
成等比数列,设 ,(
,(  )
)(1)求Tn;
(2)设
 ,求数列
,求数列 的前n项和
的前n项和 .
.(1) (2)
(2)
 (2)
(2)
(1)因为
 成等比数列,可得
成等比数列,可得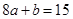 和
和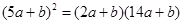
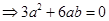 ,从而可解出a,b的值,进而得到
,从而可解出a,b的值,进而得到 ,所以
,所以 ,再根据等差数列的前n项和公式求和即可.
,再根据等差数列的前n项和公式求和即可.
(2) 由于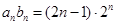 ,所以其前n项和易采用错位相减的方法求和.
,所以其前n项和易采用错位相减的方法求和.
解:(1)设
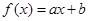 ,(
,(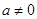 )由
)由
 成等比数列得
成等比数列得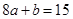 ,----------------①,
,----------------①,  得
得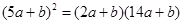
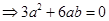
∵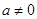 ∴
∴ ---------------② 由①②得
---------------② 由①②得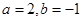 , ∴
, ∴
∴ ,显然数列
,显然数列 是首项
是首项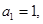 公差
公差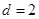 的等差数列
的等差数列
∴Tn=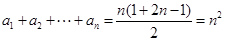
(2)∵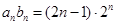
∴ =
=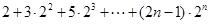
2 =
=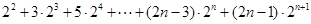
- =
= =
=
∴ =
= .
.

 成等比数列,可得
成等比数列,可得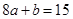 和
和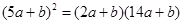
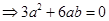 ,从而可解出a,b的值,进而得到
,从而可解出a,b的值,进而得到 ,所以
,所以 ,再根据等差数列的前n项和公式求和即可.
,再根据等差数列的前n项和公式求和即可.(2) 由于
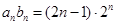 ,所以其前n项和易采用错位相减的方法求和.
,所以其前n项和易采用错位相减的方法求和.解:(1)设

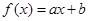 ,(
,(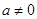 )由
)由
 成等比数列得
成等比数列得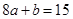 ,----------------①,
,----------------①,  得
得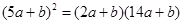
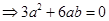
∵
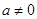 ∴
∴ ---------------② 由①②得
---------------② 由①②得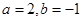 , ∴
, ∴
∴
 ,显然数列
,显然数列 是首项
是首项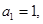 公差
公差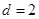 的等差数列
的等差数列∴Tn=
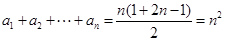
(2)∵
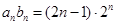
∴
 =
=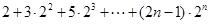
2
 =
=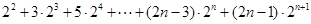
-
 =
= =
=
∴
 =
= .
.
练习册系列答案
相关题目
 的前
的前 项和
项和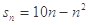 ,
,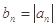 求 数列
求 数列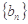 的前
的前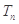 。
。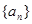 的前
的前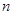 项和为
项和为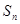 ,已知
,已知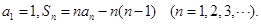
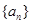 为等差数列,并写出
为等差数列,并写出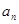 关于
关于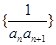 前
前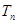 ,问满足
,问满足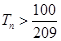 的最小正整数
的最小正整数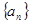 中,
中, 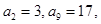 求
求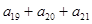 的值。
的值。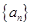 满足
满足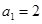 ,
,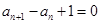
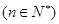 ,则此数列的通项
,则此数列的通项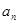 等于( )
等于( )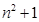
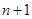
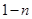
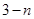
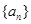 是一个公差为2的等差数列,
是一个公差为2的等差数列,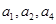 成等比数列.
成等比数列.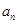 ;
;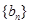 满足
满足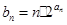 ,设
,设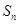 ,求
,求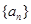 的前
的前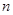 项和为
项和为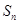 .若
.若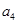 是
是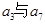 的等比中项,S10="60" ,则S20等于 _________
的等比中项,S10="60" ,则S20等于 _________ 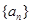 中,
中,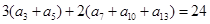 ,则此数列前13项的和为( )
,则此数列前13项的和为( )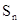 ,若
,若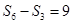 ,则
,则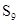 =____________.
=____________.