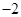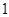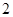题目内容
设数列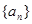 的前
的前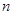 项和为
项和为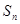 ,已知
,已知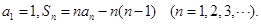
(Ⅰ)求证:数列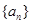 为等差数列,并写出
为等差数列,并写出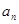 关于
关于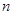 的表达式;
的表达式;
(Ⅱ)若数列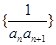 前
前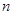 项和为
项和为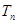 ,问满足
,问满足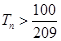 的最小正整数
的最小正整数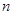 是多少?
是多少?
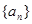 的前
的前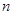 项和为
项和为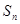 ,已知
,已知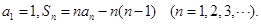
(Ⅰ)求证:数列
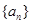 为等差数列,并写出
为等差数列,并写出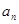 关于
关于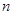 的表达式;
的表达式;(Ⅱ)若数列
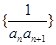 前
前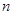 项和为
项和为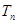 ,问满足
,问满足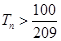 的最小正整数
的最小正整数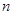 是多少?
是多少? (Ⅰ)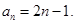 (Ⅱ)满足
(Ⅱ)满足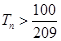 的最小正整数为12.
的最小正整数为12.
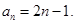 (Ⅱ)满足
(Ⅱ)满足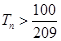 的最小正整数为12.
的最小正整数为12. (I)由当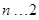 时,
时,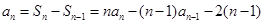 ,
,
得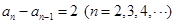 .可知数列
.可知数列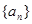 是以
是以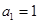 为首项,2为公差的等差数列.
为首项,2为公差的等差数列.
(II)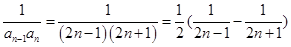 ,显然裂项求和的方法求和.
,显然裂项求和的方法求和.
解:(Ⅰ)当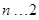 时,
时,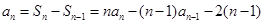 ,
,
得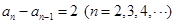 .
.
所以数列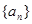 是以
是以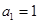 为首项,2为公差的等差数列. ……5分
为首项,2为公差的等差数列. ……5分
所以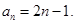 ……………………6分
……………………6分
(Ⅱ)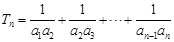
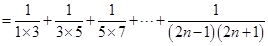
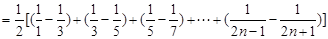
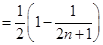
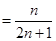 ……………10分
……………10分
由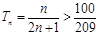 ,得
,得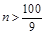 ,
,
满足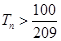 的最小正整数为12. …………………12分
的最小正整数为12. …………………12分
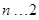 时,
时,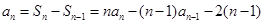 ,
, 得
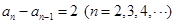 .可知数列
.可知数列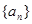 是以
是以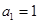 为首项,2为公差的等差数列.
为首项,2为公差的等差数列.(II)
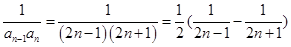 ,显然裂项求和的方法求和.
,显然裂项求和的方法求和.解:(Ⅰ)当
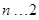 时,
时,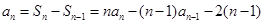 ,
, 得
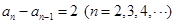 .
. 所以数列
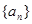 是以
是以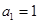 为首项,2为公差的等差数列. ……5分
为首项,2为公差的等差数列. ……5分 所以
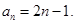 ……………………6分
……………………6分 (Ⅱ)
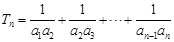
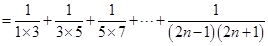
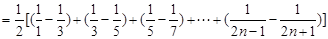
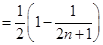
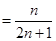 ……………10分
……………10分由
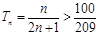 ,得
,得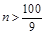 ,
,满足
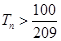 的最小正整数为12. …………………12分
的最小正整数为12. …………………12分
练习册系列答案
相关题目
 }中,
}中,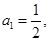 对一切
对一切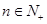 ,点
,点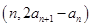 在直线y=x上,
在直线y=x上, 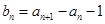 ,求证数列
,求证数列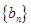 是等比数列,并求通项
是等比数列,并求通项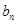 (4分);
(4分);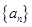 的通项公式
的通项公式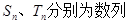
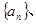
 的前n项和,是否存在常数
的前n项和,是否存在常数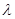 ,使得数列
,使得数列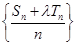 为等差数列?若存在,试求出
为等差数列?若存在,试求出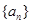 的前n项和为
的前n项和为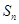 ,且
,且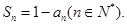
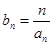 ,试求数列
,试求数列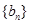 的前
的前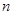 项和.
项和.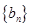 中,
中,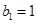 ,且点
,且点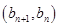 在直线
在直线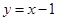 上.数列
上.数列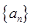 中,
中,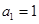 ,
,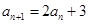 ,
,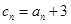 ,求数列
,求数列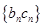 的前
的前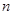 项和
项和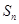 .
.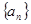 的前
的前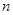 项和为
项和为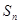 ,若
,若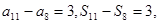 则使
则使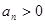 的最小正整数
的最小正整数 是一次函数,且
是一次函数,且
 成等比数列,设
成等比数列,设 ,(
,(  )
) ,求数列
,求数列 的前n项和
的前n项和 .
.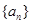 满足
满足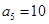 ,且
,且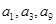 成等比数列。
成等比数列。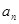 ;
;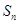 为数列
为数列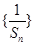 的前n项和
的前n项和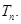
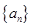 中,若
中,若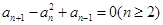 ,
,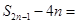 ( )
( )