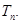题目内容
(本小题共14分)
在单调递增数列 中,
中, ,不等式
,不等式
 对任意
对任意 都成立.
都成立.
(Ⅰ)求 的取值范围;
的取值范围;
(Ⅱ)判断数列 能否为等比数列?说明理由;
能否为等比数列?说明理由;
(Ⅲ)设 ,
, ,求证:对任意的
,求证:对任意的 ,
, .
.
在单调递增数列
 中,
中, ,不等式
,不等式
 对任意
对任意 都成立.
都成立.(Ⅰ)求
 的取值范围;
的取值范围;(Ⅱ)判断数列
 能否为等比数列?说明理由;
能否为等比数列?说明理由;(Ⅲ)设
 ,
, ,求证:对任意的
,求证:对任意的 ,
, .
.(1)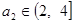 (2) 用反证法证明:假设数列
(2) 用反证法证明:假设数列 是公比为
是公比为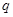 的等比数列, 因为
的等比数列, 因为 单调递增,所以
单调递增,所以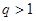 .因为
.因为 ,
,
 都成立,从而加以证明。
都成立,从而加以证明。
(3)通过前几项归纳猜想,然后运用数学归纳法加以证明。
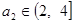 (2) 用反证法证明:假设数列
(2) 用反证法证明:假设数列 是公比为
是公比为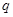 的等比数列, 因为
的等比数列, 因为 单调递增,所以
单调递增,所以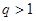 .因为
.因为 ,
,
 都成立,从而加以证明。
都成立,从而加以证明。(3)通过前几项归纳猜想,然后运用数学归纳法加以证明。
试题分析:(Ⅰ)解:因为
 是单调递增数列,
是单调递增数列,所以
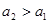 ,
,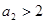 .
.令
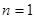 ,
,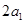
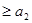 ,
,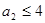 ,
,所以
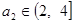 . ………………4分
. ………………4分 (Ⅱ)证明:数列
 不能为等比数列.
不能为等比数列.用反证法证明:
假设数列
 是公比为
是公比为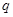 的等比数列,
的等比数列,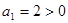 ,
,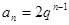 .
.因为
 单调递增,所以
单调递增,所以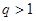 .
.因为
 ,
,
 都成立.
都成立.所以
 ,
,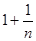
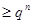 ①
①因为
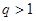 ,所以
,所以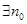
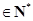 ,使得当
,使得当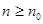 时,
时,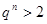 .
.因为
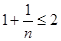
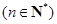 .
.所以
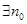
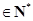 ,当
,当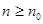 时,
时,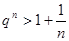 ,与①矛盾,故假设不成立.………9分
,与①矛盾,故假设不成立.………9分(Ⅲ)证明:观察:
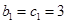 ,
,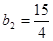
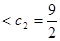 ,
,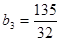
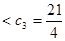 ,…,猜想:
,…,猜想: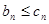 .
.用数学归纳法证明:
(1)当
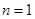 时,
时,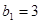
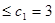 成立;
成立;(2)假设当
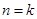 时,
时, 成立;
成立;当
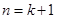 时,
时,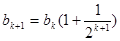
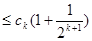

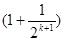
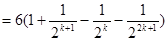
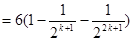
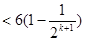
所以
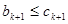 .
.根据(1)(2)可知,对任意
 ,都有
,都有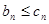 ,即
,即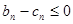 .
.由已知得,
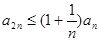 .
.所以
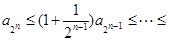
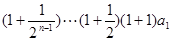 .
.所以当
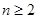 时,
时,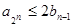
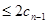
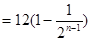
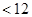 .
.因为
 .
.所以对任意

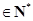 ,
, .
.对任意

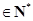 ,存在
,存在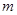
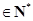 ,使得
,使得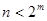 ,
,因为数列{
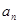 }单调递增,
}单调递增,所以
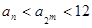 ,
,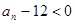 .
.因为
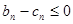 ,
,所以
 . ………………14分
. ………………14分点评:解决数列的单调性问题,要根据定义法来说明,同时要对于正面证明比较难的试题,要正难则反,属于中档题。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
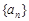 公差
公差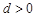 ,前n项和为
,前n项和为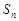 .则“
.则“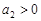 ”是“数列
”是“数列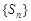 为递增数列”的
为递增数列”的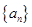 的前
的前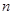 项和是
项和是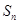 ,若
,若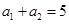 ,
,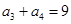 ,则
,则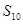 的值为( )
的值为( )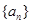 是公比
是公比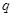 大于1的等比数列,
大于1的等比数列,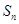 为数列
为数列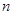 项和,已知
项和,已知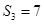 ,且
,且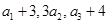 构成等差数列.
构成等差数列.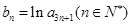 ,求数列
,求数列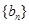 的前
的前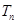 .
. 满足
满足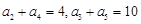 ,则它的前10项和
,则它的前10项和 ______
______ 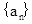 满足:
满足: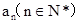 是整数,且
是整数,且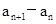 是关于x的方程
是关于x的方程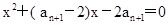 的根.
的根.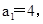 且n≥2时,
且n≥2时,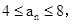 求数列{an}的前100项和S100;
求数列{an}的前100项和S100;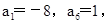 且
且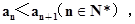 求数列
求数列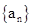 的通项公式.
的通项公式. }满足
}满足 ,且
,且 ,则
,则 的值是( )
的值是( )

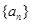 的前
的前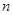 项和为
项和为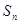 ,且
,且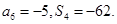
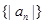 的前
的前