题目内容
已知直线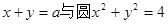 交于A、B两点,O是坐标原点,向量
交于A、B两点,O是坐标原点,向量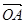 、
、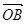 满足
满足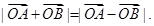 ,则实数a的值是 ( )
,则实数a的值是 ( )
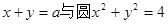 交于A、B两点,O是坐标原点,向量
交于A、B两点,O是坐标原点,向量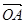 、
、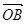 满足
满足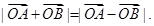 ,则实数a的值是 ( )
,则实数a的值是 ( )| A.2 | B.-2 | C.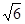 或- 或-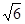 | D.2或-2 |
D
先由向量关系推出OA⊥OB,结合直线方程推出A、B两点在坐标轴上,然后求得a的值.
解:由向量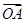 、
、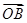 满足|
满足|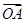 +
+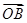 |=|
|=|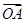 -
-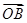 |
|
得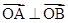 ,因为直线x+y=a的斜率是-1,
,因为直线x+y=a的斜率是-1,
所以A、B两点在坐标轴上并且在圆上,所以(0,2)和(0,-2)点都适合直线的方程,a=±2;
故选D.
考查直线和圆的方程的应用,向量的模的有关知识,是基础题.
解:由向量
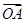 、
、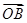 满足|
满足|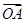 +
+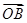 |=|
|=|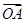 -
-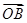 |
|得
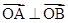 ,因为直线x+y=a的斜率是-1,
,因为直线x+y=a的斜率是-1,所以A、B两点在坐标轴上并且在圆上,所以(0,2)和(0,-2)点都适合直线的方程,a=±2;
故选D.
考查直线和圆的方程的应用,向量的模的有关知识,是基础题.

练习册系列答案
相关题目
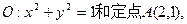 由⊙O外一点P(a,b)向⊙O引切线PQ,切点为Q,且满足
由⊙O外一点P(a,b)向⊙O引切线PQ,切点为Q,且满足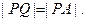 (1)求实数a,b间满足的等量关系;(2)求线段PQ长的最小值;
(1)求实数a,b间满足的等量关系;(2)求线段PQ长的最小值;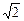 (x+y)+1+m=0与圆x2+y2=m的位置关系为
(x+y)+1+m=0与圆x2+y2=m的位置关系为 ,集合
,集合 ,
, ,则集合
,则集合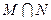 的面积是
的面积是 



 的圆心和半径分别( )
的圆心和半径分别( )



 与圆
与圆 相切,则
相切,则 的值为( )
的值为( )


