题目内容
如图，已知椭圆Γ：| x2 |
| a2 |
| y2 |
| b2 |
| F1Q |
| PM |
| MF1 |
| MF2 |
（Ⅰ）求点M的轨迹C的方程；
（Ⅱ）设不过原点O的直线l与轨迹C交于A，B两点，若直线OA，AB，OB的斜率依次成等比数列，求△OAB面积的取值范围．
分析：（Ⅰ）设M（x，y）为轨迹C上的任意一点，分类讨论，利用
•
=0，|
|≠0，即可求点M的轨迹C的方程；
（Ⅱ）由题意可知，直线l的斜率存在且不为0，可设直线l的方程，代入圆的方程，利用韦达定理及直线OA，AB，OB的斜率依次成等比数列，可求直线方程，从而可求△OAB面积，进而可得△OAB面积的取值范围．
| PM |
| MF1 |
| MF2 |
（Ⅱ）由题意可知，直线l的斜率存在且不为0，可设直线l的方程，代入圆的方程，利用韦达定理及直线OA，AB，OB的斜率依次成等比数列，可求直线方程，从而可求△OAB面积，进而可得△OAB面积的取值范围．
解答：解：（Ⅰ）设M（x，y）为轨迹C上的任意一点．
当|
|=0时，点（a，0）和点（-a，0）在轨迹C上．
当|
|≠0且|
|≠0时，由
•
=0，得
⊥
．
又|
|=|
|，所以M为线段F2Q的中点．在△QF1F2中，|
|=
|
|=a，所以有x2+y2=a2．
综上所述，点M的轨迹C的方程是x2+y2=a2．
（Ⅱ）由题意可知，直线l的斜率存在且不为0，故可设直线l的方程为y=kx+m（m≠0），A（x1，y1），B（x2，y2），
由
消去y并整理，得（1+k2）x2+2kmx+m2-a2=0，
则△=4k2m2-4（1+k2）（m2-a2）=4（k2a2+a2-m2）＞0，且x1+x2=
，x1x2=
．
∴y1y2=（kx1+m）（kx2+m）=k2x1x2+km（x1+x2）+m2．
∵直线OA，AB，OB的斜率依次成等比数列，∴
•
=
=k2，即
+m2=0，
又m≠0，
∴k2=1，即k=±1．
设点O到直线l的距离为d，则d=
，
∴S△OAB=
|AB|d=
|x1-x2|•
=
|x1-x2||m|=
．
由直线OA，OB的斜率存在，且△＞0，得0＜m2＜2a2且m2≠a2，
∴0＜
＜
=a2．
故△OAB面积的取值范围为（0，
a2）
当|
| PM |
当|
| PM |
| MF2 |
| PM |
| MF2 |
| PM |
| MF2 |
又|
| PQ |
| PF2 |
| OM |
| 1 |
| 2 |
| F1Q |
综上所述，点M的轨迹C的方程是x2+y2=a2．
（Ⅱ）由题意可知，直线l的斜率存在且不为0，故可设直线l的方程为y=kx+m（m≠0），A（x1，y1），B（x2，y2），
由
|
则△=4k2m2-4（1+k2）（m2-a2）=4（k2a2+a2-m2）＞0，且x1+x2=
| -2km |
| 1+k2 |
| m2-a2 |
| 1+k2 |
∴y1y2=（kx1+m）（kx2+m）=k2x1x2+km（x1+x2）+m2．
∵直线OA，AB，OB的斜率依次成等比数列，∴
| y1 |
| x1 |
| y2 |
| x2 |
| k2x1x2+km(x1+x2)+m2 |
| x1x2 |
| -2k2m2 |
| 1+k2 |
又m≠0，
∴k2=1，即k=±1．
设点O到直线l的距离为d，则d=
| |m| | ||
|
∴S△OAB=
| 1 |
| 2 |
| 1 |
| 2 |
| 1+k2 |
| |m| | ||
|
| 1 |
| 2 |
| 1 |
| 2 |
| m2(2a2-m2) |
由直线OA，OB的斜率存在，且△＞0，得0＜m2＜2a2且m2≠a2，
∴0＜
| m2(2a2-m2) |
| m2+(2a2-m2) |
| 2 |
故△OAB面积的取值范围为（0，
| 1 |
| 2 |
点评：本题考查椭圆的标准方程，考查直线与圆的位置关系，考查求三角形的面积，考查类比思想，解题的关键是挖掘隐含条件，正确表示三角形的面积，属于中档题．
练习册系列答案
相关题目
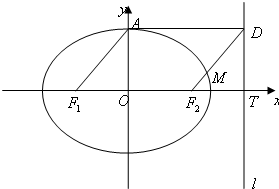如图，已知椭圆
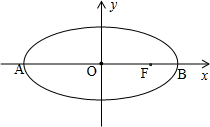在平面直角坐标系xoy中，如图，已知椭圆
如图，已知椭圆C：
（2012•江苏二模）如图，已知椭圆C：
如图，已知椭圆