题目内容
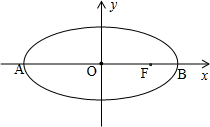 在平面直角坐标系xoy中,如图,已知椭圆
在平面直角坐标系xoy中,如图,已知椭圆| x2 |
| 9 |
| y2 |
| 5 |
(1)设动点P满足PF2-PB2=4,求点P的轨迹;
(2)设x1=2,x2=
| 1 |
| 3 |
(3)设t=9,求证:直线MN必过x轴上的一定点(其坐标与m无关).
分析:(1)设点P(x,y),由两点距离公式将PF2-PB2=4,变成坐标表示式,整理即得点P的轨迹方程.
(2)将x1=2,x2=
分别代入椭圆方程,解出点M与点N的坐标由两点式写出直线AM与直线BN的方程联立解出交点T的坐标.(3)方法一求出直线方程的参数表达式,然后求出其与x的交点的坐标,得到其横坐标为一个常数,从而说明直线过x轴上的定点.
方法二根据特殊情况即直线与x轴垂直时的情况求出定点,然后证明不垂直于x轴时两线DM与DN斜率相等,说明直线MN过该定点.
(2)将x1=2,x2=
| 1 |
| 3 |
方法二根据特殊情况即直线与x轴垂直时的情况求出定点,然后证明不垂直于x轴时两线DM与DN斜率相等,说明直线MN过该定点.
解答: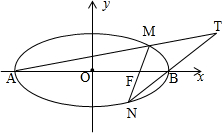 解:(1)设点P(x,y),则:F(2,0)、B(3,0)、A(-3,0).
解:(1)设点P(x,y),则:F(2,0)、B(3,0)、A(-3,0).
由PF2-PB2=4,得(x-2)2+y2-[(x-3)2+y2]=4,化简得x=
.
故所求点P的轨迹为直线x=
.
(2)将x1=2,x2=
分别代入椭圆方程,以及y1>0,y2<0,
得M(2,
)、N(
,-
)
直线MTA方程为:
=
,即y=
x+1,
直线NTB方程为:
=
,即y=
x-
.
联立方程组,解得:
,
所以点T的坐标为(7,
).
(3)点T的坐标为(9,m)
直线MTA方程为:
=
,即y=
(x+3),
直线NTB方程为:
=
,即y=
(x-3).
分别与椭圆
+
=1联立方程组,同时考虑到x1≠-3,x2≠3,
解得:M(
,
)、N(
,-
).
(方法一)当x1≠x2时,
直线MN方程为:
=
令y=0,解得:x=1.此时必过点D(1,0);
当x1=x2时,直线MN方程为:x=1,与x轴交点为D(1,0).
所以直线MN必过x轴上的一定点D(1,0).
(方法二)若x1=x2,则由
=
及m>0,得m=2
,
此时直线MN的方程为x=1,过点D(1,0).
若x1≠x2,则m≠2
,直线MD的斜率kMD=
=
,
直线ND的斜率kND=
=
,得kMD=kND,所以直线MN过D点.
因此,直线MN必过x轴上的点(1,0).
 解:(1)设点P(x,y),则:F(2,0)、B(3,0)、A(-3,0).
解:(1)设点P(x,y),则:F(2,0)、B(3,0)、A(-3,0).由PF2-PB2=4,得(x-2)2+y2-[(x-3)2+y2]=4,化简得x=
| 9 |
| 2 |
故所求点P的轨迹为直线x=
| 9 |
| 2 |
(2)将x1=2,x2=
| 1 |
| 3 |
得M(2,
| 5 |
| 3 |
| 1 |
| 3 |
| 20 |
| 9 |
直线MTA方程为:
| y-0 | ||
|
| x+3 |
| 2+3 |
| 1 |
| 3 |
直线NTB方程为:
| y-0 | ||
-
|
| x-3 | ||
|
| 5 |
| 6 |
| 5 |
| 2 |
联立方程组,解得:
|
所以点T的坐标为(7,
| 10 |
| 3 |
(3)点T的坐标为(9,m)
直线MTA方程为:
| y-0 |
| m-0 |
| x+3 |
| 9+3 |
| m |
| 12 |
直线NTB方程为:
| y-0 |
| m-0 |
| x-3 |
| 9-3 |
| m |
| 6 |
分别与椭圆
| x2 |
| 9 |
| y2 |
| 5 |
解得:M(
| 3(80-m2) |
| 80+m2 |
| 40m |
| 80+m2 |
| 3(m2-20) |
| 20+m2 |
| 20m |
| 20+m2 |
(方法一)当x1≠x2时,
直线MN方程为:
y+
| ||||
|
x-
| ||||
|
令y=0,解得:x=1.此时必过点D(1,0);
当x1=x2时,直线MN方程为:x=1,与x轴交点为D(1,0).
所以直线MN必过x轴上的一定点D(1,0).
(方法二)若x1=x2,则由
| 240-3m2 |
| 80+m2 |
| 3m2-60 |
| 20+m2 |
| 10 |
此时直线MN的方程为x=1,过点D(1,0).
若x1≠x2,则m≠2
| 10 |
| ||
|
| 10m |
| 40-m2 |
直线ND的斜率kND=
| ||
|
| 10m |
| 40-m2 |
因此,直线MN必过x轴上的点(1,0).
点评:本小题主要考查求简单曲线的方程,考查方直线与椭圆的方程等基础知识.考查运算求解能力和探究问题的能力

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
 如图,在平面直角坐标系xOy中,锐角α和钝角β的终边分别与单位圆交于A,B两点.若点A的横坐标是
如图,在平面直角坐标系xOy中,锐角α和钝角β的终边分别与单位圆交于A,B两点.若点A的横坐标是