题目内容
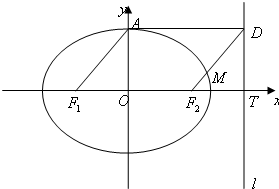 如图,已知椭圆
如图,已知椭圆| x2 |
| a2 |
| y2 |
| b2 |
(1)求椭圆的离心率;
(2)设线段F2D与椭圆交于点M,是否存在实数λ,使
| TA |
| TM |
(3)若B是直线l上一动点,且△AF2B外接圆面积的最小值是4π,求椭圆方程.
分析:(1)由AD=F1F2得到a与c的关系
=2c进而得到e=
.
(2)得到a,b,c的关系且设出各点的坐标可得
=(-2c,c),直线F2D的方程是x-y-c=0联立直线与椭圆的方程得M(
c,
c),进而得到
=3
.
(3)设圆心N的坐标为(n,n),圆过准线上一点B,则圆与准线有公共点所以
≥|n-2c|可得n≤-3c或n≥c又r2=(n-c)2+n2=2(n-
)2+
∈[c2,+∞)
(πr2)min=c2π=4π,则c2=4.
| a2 |
| c |
| ||
| 2 |
(2)得到a,b,c的关系且设出各点的坐标可得
| TA |
| 4 |
| 3 |
| 1 |
| 3 |
| TA |
| TM |
(3)设圆心N的坐标为(n,n),圆过准线上一点B,则圆与准线有公共点所以
| (n-c)2+n2 |
| c |
| 2 |
| c2 |
| 2 |
(πr2)min=c2π=4π,则c2=4.
解答:解:(1)依题意:AD=F1F2,即
=2c,
所以离心率e=
.
(2)由(Ⅰ)知:a=
c,b=c,
故A(0,c),D(2c,c),F2(c,0),T(2c,0),
=(-2c,c)
所以椭圆方程是
+
=1,即x2+2y2=2c2,
直线F2D的方程是x-y-c=0
由,{
解得:,{
(舍去)或,{
即M(
c,
c),
=(-
c,
c),所以
=3
,
即存在λ=3使
=3
成立.
(3)由题可知圆心N在直线y=x上,设圆心N的坐标为(n,n),
因圆过准线上一点B,则圆与准线有公共点,
设圆心N到准线的距离为d,则NF2≥d,即
≥|n-2c|,
解得:n≤-3c或n≥c,
又r2=(n-c)2+n2=2(n-
)2+
∈[c2,+∞)
由题可知,(πr2)min=c2π=4π,则c2=4,
故椭圆的方程为
+
=1.
| a2 |
| c |
所以离心率e=
| ||
| 2 |
(2)由(Ⅰ)知:a=
| 2 |
故A(0,c),D(2c,c),F2(c,0),T(2c,0),
| TA |
所以椭圆方程是
| x2 |
| 2c2 |
| y2 |
| c2 |
直线F2D的方程是x-y-c=0
由,{
|
|
|
即M(
| 4 |
| 3 |
| 1 |
| 3 |
| TM |
| 2 |
| 3 |
| 1 |
| 3 |
| TA |
| TM |
即存在λ=3使
| TA |
| TM |
(3)由题可知圆心N在直线y=x上,设圆心N的坐标为(n,n),
因圆过准线上一点B,则圆与准线有公共点,
设圆心N到准线的距离为d,则NF2≥d,即
| (n-c)2+n2 |
解得:n≤-3c或n≥c,
又r2=(n-c)2+n2=2(n-
| c |
| 2 |
| c2 |
| 2 |
由题可知,(πr2)min=c2π=4π,则c2=4,
故椭圆的方程为
| x2 |
| 8 |
| y2 |
| 4 |
点评:本题的重点是依向量为载体考查直线与圆锥曲线的相交问题,即联立直线椭圆的方程求解即可,还考查了焦点三角形面积的知识点,这些都是高考的重点内容.

练习册系列答案
相关题目
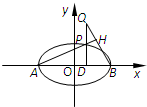 如图,已知椭圆
如图,已知椭圆 (2013•汕头一模)如图.已知椭圆
(2013•汕头一模)如图.已知椭圆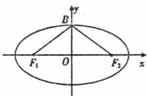 (2012•安徽模拟)如图,已知椭圆
(2012•安徽模拟)如图,已知椭圆 (2011•崇明县二模)如图,已知椭圆
(2011•崇明县二模)如图,已知椭圆 如图,已知椭圆
如图,已知椭圆