题目内容
如图,在直三棱柱 中,
中, ,
, ,异面直线
,异面直线 与
与 所成
所成
的角为 .
.

(Ⅰ)求证: ;
;
(Ⅱ)设 是
是 的中点,求
的中点,求 与平面
与平面 所成角的正弦值.
所成角的正弦值.
 中,
中, ,
, ,异面直线
,异面直线 与
与 所成
所成的角为
 .
.
(Ⅰ)求证:
 ;
;(Ⅱ)设
 是
是 的中点,求
的中点,求 与平面
与平面 所成角的正弦值.
所成角的正弦值.(Ⅰ)详见解析;(Ⅱ)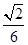 .
.
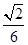 .
.试题分析:(Ⅰ)由直三棱柱的性质证
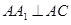 ,再证明
,再证明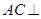 平面
平面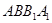 ;(Ⅱ)用向量法求解.
;(Ⅱ)用向量法求解.试题解析:(Ⅰ)
 三棱柱
三棱柱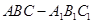 是直三棱柱,
是直三棱柱,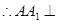 平面
平面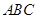 ,
,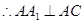 .
.又
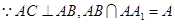 ,
,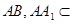 平面
平面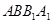 ,
,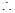
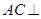 平面
平面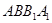 ,
,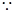
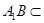 平面
平面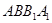 ,
,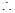
 . (5分)
. (5分)(Ⅱ)如图,
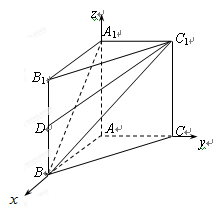
以
 点为原点,
点为原点,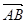 、
、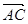 、
、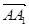 分别为
分别为 、
、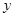 、
、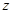 轴正方向,
轴正方向,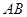 线段长为单位长,
线段长为单位长,建立空间直角坐标系,设
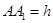 ,则
,则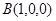 ,
,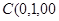 ,
,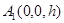 ,
,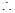
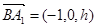 ,
,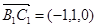 ,
,由于直线
 与
与 所成的角为
所成的角为 .
.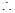
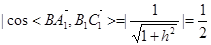 ,解得
,解得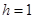 ,
,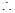
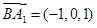 ,
,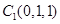 ,
,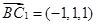 设平面
设平面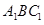 的法向量
的法向量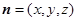 ,
,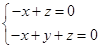 ,可取
,可取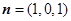 .
.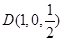 ,
,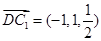 . (10分)
. (10分)于是
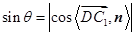
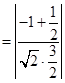
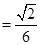 ,
,所以
 与平面
与平面 所成角的正弦值为
所成角的正弦值为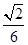 . (12分)
. (12分)
练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案
相关题目
 .
.
 与平面
与平面 所成角的正弦值;
所成角的正弦值; 上是否存在点
上是否存在点 ?使得二面角
?使得二面角 的大小为60°,若存在,求出
的大小为60°,若存在,求出 的长;若不存在,请说明理由.
的长;若不存在,请说明理由. ,
, ,
, ,
, ,
, 是
是 的中点.
的中点.
 ;
; 的平面角的正弦值.
的平面角的正弦值. 中,点
中,点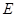 是
是 的中点,点
的中点,点 是
是 的中点,将△
的中点,将△ 、△
、△ 分别沿
分别沿 、
、 折起,使
折起,使 、
、 两点重合于点
两点重合于点 ,连接
,连接 ,
, .
.

 ; (2)求点
; (2)求点 的距离.
的距离. 的正方形
的正方形 中,
中, 分别为
分别为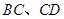 的中点,
的中点, 分别为
分别为 的中点,现沿
的中点,现沿 折叠,使
折叠,使 三点重合,重合后的点记为
三点重合,重合后的点记为 ,构成一个三棱锥.
,构成一个三棱锥.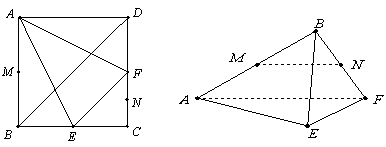
 与平面
与平面 的位置关系,并给出证明;
的位置关系,并给出证明; 平面
平面 ;
; 的体积.
的体积.

 、
、 和平面
和平面 ,若
,若 ,则“
,则“ ”是“
”是“ ”的( )
”的( ) a,则l//a ;② l//a,m//a 则 l//m; ③a丄β,l
a,则l//a ;② l//a,m//a 则 l//m; ③a丄β,l 则
则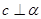 ;②。若
;②。若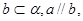 则
则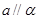 ;
;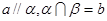 ,则
,则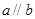 ; ④。若
; ④。若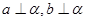 ,则
,则