题目内容
如果数据 、
、 、……
、…… 的平均值为
的平均值为 ,方差为
,方差为 ,则
,则 ,
, ,……
,……  的平均值和方差分别为( )
的平均值和方差分别为( )
A. 和 和 | B.3 +5和9 +5和9 |
C.3 +5和 +5和 | D.3 +5 和9 +5 和9 +30 +30 +25 +25 |
B
解析试题分析:先根据平均值和方差的定义表示出数据x1、x2、…、xn的平均值 和方差sn,然后分别表示出3x1+5、3x2+5、…、3xn+5的平均值和方差,整体代入可得值.那么结合均值的性质可知,
和方差sn,然后分别表示出3x1+5、3x2+5、…、3xn+5的平均值和方差,整体代入可得值.那么结合均值的性质可知, ,则3x1+5、3x2+5、…、3xn+5的平均值为
,则3x1+5、3x2+5、…、3xn+5的平均值为 ,因此排除答案A,然后借助于方差公式可知为9
,因此排除答案A,然后借助于方差公式可知为9 ,故答案为B.
,故答案为B.
考点:平均值和方差
点评:考查学生会求一组数据的平均值和方差,会利用整体代入的数学思想解决数学问题.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
设有一个线性回归方程为 ,则变量
,则变量 增加一个单位时 ( )
增加一个单位时 ( )
A. 平均增加2.5个单位 平均增加2.5个单位 | B. 平均增加3个单位 平均增加3个单位 |
C. 平均减少2.5个单位 平均减少2.5个单位 | D. 平均减少3个单位 平均减少3个单位 |
对于线性相关系数 ,叙述正确的是
,叙述正确的是
A.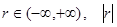 越大,相关程度越大,反之相关程度越小 越大,相关程度越大,反之相关程度越小 |
B. 越大,相关程度越大,反之相关程度越小 越大,相关程度越大,反之相关程度越小 |
C.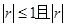 越接近1,相关程度越大 越接近1,相关程度越大 |
| D.以上说法都不对 |
为了解一片速生林的生长情况,随机测量了其中100株树木的底部周长(单位:cm).根据所得数据画出了样本的频率分布直方图,那么在这100株树木中,底部周长小于110cm的株数是
| A.30 | B.60 |
| C.70 | D.80 |
现有60件产品,编号从1到60,若用系统抽样方法从中抽取6件检验,则所抽到的个体编号可能是
| A.5,10,15,20,25,30 | B.2,14,26,28,42,56 |
| C.5,8,31,36,48,54 | D.3,13,23,33,43,53 |
为了了解某校高三学生的视力情况,随机地抽查了该校100名高三学生,得到学生视力频率分布直方图,如右图,由于不慎将部分数据丢失,但知道前4组的频数成等比数列,后6组的频率成等差数列.设最大频率为a;视力在4.6到5.0之间的学生人数为b,则a、b的值分别为
| A.0.27,78 | B.0.27,83 |
| C.2.7,78 | D.2.7,83 |
 =1.23x+4 B.
=1.23x+4 B.