Question

【题目】对于两个定义域相同的函数f（x），g（x），若存在实数m、n使h（x）=mf（x）+ng（x），则称函数h（x）是由“基函数f（x），g（x）”生成的．
（1）若f（x）=x2+3x和个g（x）=3x+4生成一个偶函数h（x），求h（2）的值；
（2）若h（x）=2x2+3x﹣1由函数f（x）=x2+ax，g（x）=x+b（a、b∈R且ab≠0）生成，求a+2b的取值范围；
（3）利用“基函数f（x）=log4（4x+1），g（x）=x﹣1”生成一个函数h（x），使之满足下列件：①是偶函数；②有最小值1；求函数h（x）的解析式并进一步研究该函数的单调性（无需证明）．

Answer 1

【答案】
（1）解：设h（x）=m（x2+3x）+n（3x+4）=mx2+3（m+n）x+4n，

∵h（x）是偶函数，∴m+n=0，∴h（2）=4m+4n=0；

（2）解：设h（x）=2x2+3x﹣1=m（x2+ax）+n（x+b）=mx2+（am+n）x+nb

∴ 得

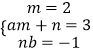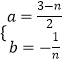
∴a+2b= ﹣ = ﹣ ﹣

由ab≠0知，n≠3，

∴a+2b∈

（3）解：设h（x）=mlog4（4x+1）+n（x﹣1）

∵h（x）是偶函数，∴h（﹣x）﹣h（x）=0，

即mlog4（4﹣x+1）+n（﹣x﹣1）﹣mlog4（4x+1）﹣n（x﹣1）=0

∴（m+2n）x=0得m=﹣2n

则h（x）=﹣2nlog4（4x+1）+n（x﹣1）=﹣2n[log4（4x+1）﹣ ]=﹣2n[log4（2x+ ）+ ]

∵h（x）有最小值1，则必有n＜0，且有﹣2n=1∴m=1．n=

∴h（x）=log4（2x+ ）+

h（x）在[0，+∞）上是增函数，在（﹣∞，0]上是减函数．

【解析】（1）先用待定系数法表示出偶函数h（x），再根据其是偶函数这一性质得到引入参数的方程，求出参数的值，即得函数的解析式，代入自变量求值即可．（2）先用待定系数法表示出偶函数h（x），再根据同一性建立引入参数的方程求参数，然后再求a+2b的取值范围；（3）先用待定系数法表示出函数h（x），再根据函数h（x）的性质求出相关的参数，代入解析式，由解析研究出其单调性即可
【考点精析】根据题目的已知条件，利用函数的单调性和奇偶性与单调性的综合的相关知识可以得到问题的答案，需要掌握注意：函数的单调性是函数的局部性质；函数的单调性还有单调不增，和单调不减两种；奇函数在关于原点对称的区间上有相同的单调性；偶函数在关于原点对称的区间上有相反的单调性．