题目内容
【题目】已知函数f(x)=ex-m(x+1)+1(m∈R).
(1)若函数f(x)的极小值为1,求实数m的值;
(2)当x≥0时,不等式![]() 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.
【答案】(1)m=1;(2)(-∞,2]
【解析】
(1)求得![]() ,分类讨论求得函数的单调性,即可求解函数的极值;
,分类讨论求得函数的单调性,即可求解函数的极值;
(2)令![]() ,求得
,求得![]() ,令
,令![]() ,得
,得![]() ,再
,再![]() ,利用导数得到
,利用导数得到![]() 的单调性与最值,即可求解.
的单调性与最值,即可求解.
(1)由题意,函数![]() ,则
,则![]() ,
,
①若m≤0,则f'(x)>0,∴f(x)在(-∞,+∞)单调递增,所以f(x)无极值,
②若m>0,当x>lnm时,f'(x)>0,
当x<lnm时,f'(x)<0,f(x)在(-∞,lnm)单调递减,在(lnm,+∞)单调递增,
所以f(x)的极小值为f(lnm),由m-m(lnm+1)+1=1,解得m=1.
(2)令![]() (x≥0),
(x≥0),![]() ,
,
令![]() ,
,![]() ,
,
令![]() ,
,
显然p(x)在[0,+∞)单调递增,∴p(x)![]() p(0)=2-m.
p(0)=2-m.
①当m![]() 2时,p(x)
2时,p(x)![]() 0,∴h'(x)
0,∴h'(x)![]() 0,∴h(x)在[0,+∞)单调递增,
0,∴h(x)在[0,+∞)单调递增,
∴![]() ,即g'(x)
,即g'(x)![]() 0,∴g(x)在[0,+∞)单调递增,
0,∴g(x)在[0,+∞)单调递增,
所以g(x)![]() g(0)=2-m
g(0)=2-m![]() 0,此时符合题意;
0,此时符合题意;
②当m![]() 2时,p(0)<0,∴x0∈(0,+∞),使p(x0)=0,
2时,p(0)<0,∴x0∈(0,+∞),使p(x0)=0,
故p(x)在(0,x0)恒为负值,h(x)在(0,x0)单调递减,此时![]() ,
,
所以g(x)在(0,x0)单调递减,所以g(x)![]() g(0)=2-m
g(0)=2-m![]() 0,此时不符合题意,
0,此时不符合题意,
故所求m的取值范围为(-∞,2].

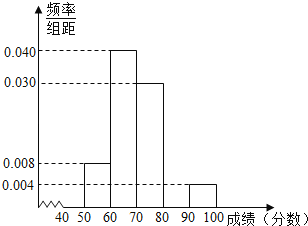
【题目】学校从参加高二年级期末考试的学生中抽出一些学生,并统计了他们的数学成绩(成绩均为整数且满分为100分),所得数据整理后,列出了如下频率分布表.
分组 | 频数 | 频率 |
[40,50) | A | 0.04 |
[50,60) | 4 | 0.08 |
[60,70) | 20 | 0.40 |
[70,80) | 15 | 0.30 |
[80,90) | 7 | B |
[90,100] | 2 | 0.04 |
合计 | C | 1 |

(1)在给出的样本频率分布表中,求A,B,C的值;
(2)补全频率分布直方图,并利用它估计全体高二年级学生期末数学成绩的众数、中位数;
(3)现从分数在[80,90),[90,100]的9名同学中随机抽取两名同学,求被抽取的两名学生分数均不低于90分的概率.
【题目】学校从参加高二年级期末考试的学生中抽出一些学生,并统计了他们的数学成绩(成绩均为整数且满分为100分),所得数据整理后,列出了如下频率分布表.
分组 | 频数 | 频率 |
[40,50) | A | 0.04 |
[50,60) | 4 | 0.08 |
[60,70) | 20 | 0.40 |
[70,80) | 15 | 0.30 |
[80,90) | 7 | B |
[90,100] | 2 | 0.04 |
合计 | C | 1 |
(1)在给出的样本频率分布表中,求A,B,C的值;
(2)补全频率分布直方图,并利用它估计全体高二年级学生期末数学成绩的众数、中位数;
(3)现从分数在[80,90),[90,100]的9名同学中随机抽取两名同学,求被抽取的两名学生分数均不低于90分的概率.