ЬтФПФкШн
ЁОЬтФПЁПвбжЊЙигкxЕФвЛдЊЖўДЮКЏЪ§fЃЈxЃЉЃНax2Љ2bx+8ЃЎ
ЃЈ1ЃЉЩшМЏКЯPЃН{1ЃЌ2ЃЌ3}КЭQЃН{2ЃЌ3ЃЌ4ЃЌ5}ЃЌЗжБ№ДгМЏКЯPКЭQжаЫцЛњШЁвЛИіЪ§зїЮЊaКЭbЃЌЧѓКЏЪ§yЃНfЃЈxЃЉдкЧјМфЃЈЉЁоЃЌ2]ЩЯгаСуЕуЧвЮЊМѕКЏЪ§ЕФИХТЪЃП
ЃЈ2ЃЉЩшМЏКЯPЃН[1ЃЌ3]КЭQ[2ЃЌ5]ЃЌЗжБ№ДгМЏКЯPКЭQжаЫцЛњШЁвЛИіЪЕЪ§зїЮЊaКЭbЃЌЧѓКЏЪ§yЃНfЃЈxЃЉдкЧјМфЃЈЉЁоЃЌ2]ЩЯгаСуЕуЧвЮЊМѕКЏЪ§ЕФИХТЪЃП
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЎЃЈ2ЃЉ
ЃЎЃЈ2ЃЉ![]() ЃЎ
ЃЎ
ЁОНтЮіЁП
(1)РћгУСаОйЗЈНсКЯЙХЕфИХаЭЕФИХТЪЙЋЪННјааМЦЫуМДПЩ;
(2)зїГіВЛЕШЪНзщЖдгІЕФЧјгђ,ЧѓГіЖдгІЧјгђЕФУцЛ§,НсКЯМИКЮИХаЭЕФИХТЪЙЋЪННјааМЦЫуМДПЩ.
(1)змЪТМўЪ§n=3ЁС4=12,
ШєТњзуy=f(x)дкЧјМф(ЉЁо,2]ЩЯгаСуЕуЧвЮЊМѕКЏЪ§,дђ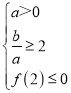 ,
,
МДТњзуЬѕМўЕФa,bЮЊ(1,3),(1,4),(1,5),(2,4),(2,5),ЙВга5Иі,
дђЖдгІЕФИХТЪP![]() ;
;
(2)гЩЬтЩшЬѕМўжЊ![]() ,
,
Шєy=f(x)дкЧјМф(ЉЁо,2]ЩЯгаСуЕуЧвЮЊМѕКЏЪ§,
дђ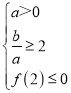 ,МД
,МД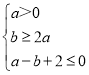 ,
,
ЖдгІЕФЧјгђШчЯТЭМЫљЪО:
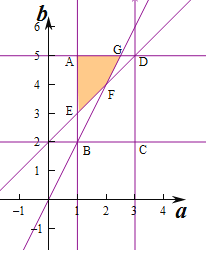
гЩ![]() ЕУ
ЕУ![]() ,МДF(2,4),
,МДF(2,4),
гЩ![]() ЕУ
ЕУ![]() ,МДE(1,3),
,МДE(1,3),
гЩ![]() ЕУ
ЕУ![]() ,МДG(
,МДG(![]() ,5),
,5),
гжA(1,5),D(3,5),
дђвѕгАВПЗжЕФУцЛ§S=SЁїAEDЉSЁїGDF![]() 2ЁС2
2ЁС2![]() (3
(3![]() )(5Љ4)=2
)(5Љ4)=2![]() ,
,
ОиаЮABCDЕФУцЛ§S=2ЁС3=6,
дђЖдгІЕФИХТЪ![]() .
.

ЁОЬтФПЁПЙЄГЇГщШЁСЫдквЛЖЮЪБМфФкЩњВњЕФвЛХњВњЦЗЃЌВтСПвЛЯюжЪСПжИБъжЕЃЌЛцжЦСЫШчЭМЫљЪОЕФЦЕТЪЗжВМжБЗНЭМ.
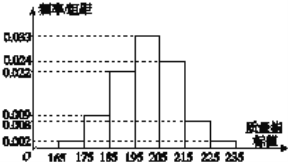
ЃЈ1ЃЉМЦЫуИУбљБОЕФЦНОљжЕ![]() ЃЌЗНВю
ЃЌЗНВю![]() ЃЛЃЈЭЌвЛзщжаЕФЪ§ОнгУИУзщЧјМфЕФжаЕужЕзїДњБэЃЉ
ЃЛЃЈЭЌвЛзщжаЕФЪ§ОнгУИУзщЧјМфЕФжаЕужЕзїДњБэЃЉ
ЃЈ2ЃЉШєжЪСПжИБъжЕдк![]() жЎФкЮЊвЛЕШЦЗ.
жЎФкЮЊвЛЕШЦЗ.
ЃЈiЃЉгУбљБОЙРМЦзмЬхЃЌЮЪИУЙЄГЇвЛЬьЩњВњЕФВњЦЗЪЧЗёга![]() вдЩЯЮЊвЛЕШЦЗЃП
вдЩЯЮЊвЛЕШЦЗЃП
ЃЈiiЃЉФГЬьдчЩЯЁЂЯТЮчЗжБ№ГщМьСЫ50МўВњЦЗЃЌЭъГЩЯТУцЕФБэИёЃЌВЂИљОнвбгаЪ§ОнЃЌХаЖЯЪЧЗёга![]() ЕФАбЮеШЯЮЊвЛЕШЦЗТЪгыЩњВњЪБМфгаЙиЃП
ЕФАбЮеШЯЮЊвЛЕШЦЗТЪгыЩњВњЪБМфгаЙиЃП
вЛЕШЦЗИіЪ§ | ЗЧвЛЕШЦЗИіЪ§ | змМЦ | |
дчЩЯ | 36 | 50 | |
ЯТЮч | 26 | 50 | |
змМЦ |
ИНЃК![]() .
.
| 0.25 | 0.15 | 0.10 | 0.050 | 0.010 | 0.001 |
| 1.323 | 2.072 | 2.706 | 3.841 | 6.635 | 10.828 |
ВЮПМЪ§ОнЃК![]() .
.

