题目内容
已知函数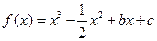 ,(1)若
,(1)若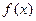 图象有与
图象有与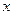 轴平行的切线,求
轴平行的切线,求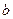 的取值范围;(2)若
的取值范围;(2)若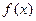 在
在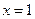 时取得极值,且
时取得极值,且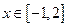 时,
时,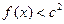 恒成立,求
恒成立,求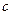 的取值范围。
的取值范围。
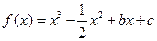 ,(1)若
,(1)若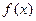 图象有与
图象有与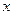 轴平行的切线,求
轴平行的切线,求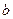 的取值范围;(2)若
的取值范围;(2)若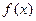 在
在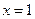 时取得极值,且
时取得极值,且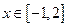 时,
时,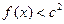 恒成立,求
恒成立,求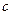 的取值范围。
的取值范围。⑴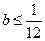 ⑵
⑵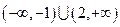
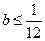 ⑵
⑵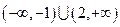
(1)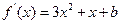 ,∵
,∵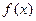 的图象上有与
的图象上有与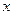 轴平行的切线,则
轴平行的切线,则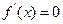 有实数解,即方程
有实数解,即方程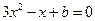 有实数解,∴
有实数解,∴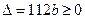 ,∴
,∴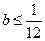 。
。
(2)由题意知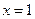 是方程
是方程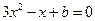 的一根,设另一根为
的一根,设另一根为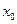 ,则
,则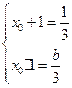
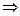
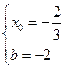 ,∴
,∴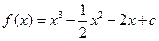 ,∴
,∴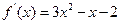 ,当
,当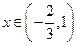 时,
时,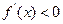 ,当
,当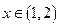 时,
时,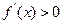 ,∴当
,∴当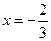 时,
时,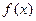 有极大值
有极大值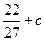 ,又
,又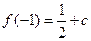 ,
,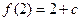 ,即当
,即当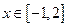 时,
时,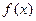 的最大值
的最大值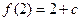 ,∵
,∵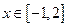 时,
时,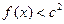 恒成立,∴
恒成立,∴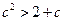 ,解得:
,解得: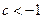 或
或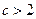 ,故
,故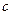 的取值范围是
的取值范围是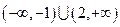 。
。
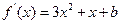 ,∵
,∵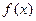 的图象上有与
的图象上有与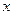 轴平行的切线,则
轴平行的切线,则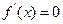 有实数解,即方程
有实数解,即方程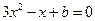 有实数解,∴
有实数解,∴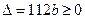 ,∴
,∴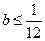 。
。(2)由题意知
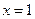 是方程
是方程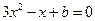 的一根,设另一根为
的一根,设另一根为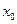 ,则
,则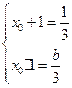
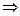
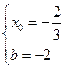 ,∴
,∴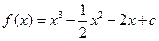 ,∴
,∴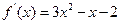 ,当
,当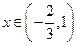 时,
时,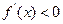 ,当
,当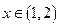 时,
时,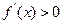 ,∴当
,∴当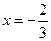 时,
时,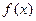 有极大值
有极大值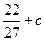 ,又
,又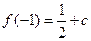 ,
,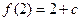 ,即当
,即当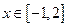 时,
时,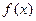 的最大值
的最大值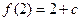 ,∵
,∵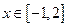 时,
时,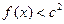 恒成立,∴
恒成立,∴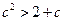 ,解得:
,解得: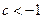 或
或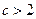 ,故
,故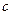 的取值范围是
的取值范围是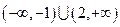 。
。
练习册系列答案
 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
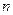 是负整数时,公式
是负整数时,公式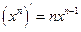 仍成立。
仍成立。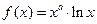 ,其中
,其中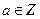 .
.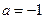 时,求函数f(x)的最大值; (2)讨论函数f(x)的单调性.
时,求函数f(x)的最大值; (2)讨论函数f(x)的单调性.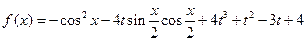 ,
,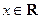 ,其中
,其中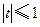 ,将
,将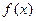 的最小值记为
的最小值记为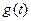 .
.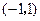 内的单调性并求极值.
内的单调性并求极值.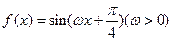 ,若
,若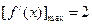 ,则
,则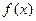 的最小正周期
的最小正周期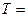 _______________.
_______________.
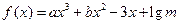 ,在
,在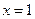 和
和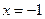 时取得极值,若对任意
时取得极值,若对任意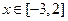 都有
都有 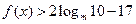 恒成立,求实数
恒成立,求实数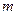 的取值集合.
的取值集合. ,若
,若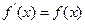 ,则
,则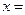 。
。 ,求
,求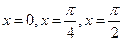 时
时 的值。
的值。