题目内容
△ABC的BC边上的高线为AD,BD=a,CD=b,且a<b,将△ABC沿AD折成大小为θ的二面角B-AD-C,若cosθ=
,则此时△ABC是( )
| a |
| b |
| A.锐角三角形 |
| B.钝角三角形 |
| C.直角三角形 |
| D.形状与a,b的值有关的三角形 |
∵AD是△ABC,BC边上的高,∴AD⊥BD,AD⊥CD,
∴∠BDC为二面角B-AD-C的平面角,∠BDC=θ
设BC=c,则c2=a2+b2-2abcosθ=a2+b2-2ab×
=b2-a2,即b2=a2+c2,
AB=
;AC=
,
∴c2=BC2=AC2-AB2,
∴折叠后△ABC为直角三角形.
故选C.
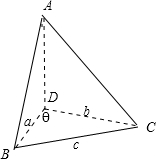
∴∠BDC为二面角B-AD-C的平面角,∠BDC=θ
设BC=c,则c2=a2+b2-2abcosθ=a2+b2-2ab×
| a |
| b |
AB=
| a2+AD2 |
| b2+AD2 |
∴c2=BC2=AC2-AB2,
∴折叠后△ABC为直角三角形.
故选C.


练习册系列答案
相关题目
 ,且AC=BC.
,且AC=BC. 平面EBC;
平面EBC; 的大小.
的大小.




 中,
中, ,
, 分别是
分别是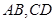 的中点,
的中点,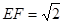 ,则异面直线
,则异面直线 与
与 所成的角为 .
所成的角为 .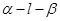 中,
中,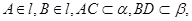 且
且 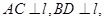 若
若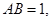
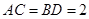 ,
, 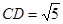 , 则二面角
, 则二面角