题目内容
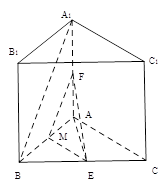
如图,在三棱锥P-ABC中,PA=PB,PA⊥PB,AB⊥BC,∠BAC=30°,平面PAB⊥平面ABC.
(Ⅰ)求证:PA⊥平面PBC;
(Ⅱ)求二面角P-AC-B的大小;
(Ⅲ)求异面直线AB和PC所成角的大小.

(Ⅰ)求证:PA⊥平面PBC;
(Ⅱ)求二面角P-AC-B的大小;
(Ⅲ)求异面直线AB和PC所成角的大小.

(Ⅰ)证明:∵平面PAB⊥平面ABC,平面PAB∩平面ABC=AB,
且BC⊥AB,∴BC⊥平面PAB.
∵PA?平面PAB,∴PA⊥BC.
又∵PA⊥PB,∴PA⊥平面PBC.
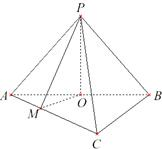
(Ⅱ)作PO⊥AB于点O,OM⊥AC于点M,连接PM.
∵平面PAB⊥平面ABC,∴PO⊥平面ABC,
根据三垂线定理得PM⊥AC,∴∠PMO是二面角P-AC-B的平面角.
设PA=PB=
,∵PA⊥PB,∴AB=2
,PO=BO=AO=
.
∵OM⊥AM,∠MAO=30°,∴OM=AO•sin30°=
,∴tanPMO=
=
=2,
即二面角P-AC-B的大小是arctan2.
(Ⅲ)在底面ABC内分别过A、C作BC、AB的平行线,交于点D,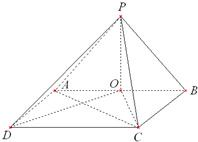
连接OC,OD,PD.
则∠PCD是异面直线AB和PC所成的角或其补角.
∵AB⊥BC,∠BAC=30°,
∴BC=AB•tan30°=2,OC=
=
,
∴PC=
=
.
易知底面ABCD为矩形,从而OC=OD,PC=PD.
在△PCD中,cosPCD=
=
,
∴异面直线AB和PC所成角的大小为arccos
.
且BC⊥AB,∴BC⊥平面PAB.
∵PA?平面PAB,∴PA⊥BC.
又∵PA⊥PB,∴PA⊥平面PBC.
(Ⅱ)作PO⊥AB于点O,OM⊥AC于点M,连接PM.
∵平面PAB⊥平面ABC,∴PO⊥平面ABC,
根据三垂线定理得PM⊥AC,∴∠PMO是二面角P-AC-B的平面角.
设PA=PB=
| 6 |
| 3 |
| 3 |
∵OM⊥AM,∠MAO=30°,∴OM=AO•sin30°=
| AO |
| 2 |
| PO |
| OM |
| AO |
| OM |
即二面角P-AC-B的大小是arctan2.
(Ⅲ)在底面ABC内分别过A、C作BC、AB的平行线,交于点D,

连接OC,OD,PD.
则∠PCD是异面直线AB和PC所成的角或其补角.
∵AB⊥BC,∠BAC=30°,
∴BC=AB•tan30°=2,OC=
| OB2+BC2 |
| 7 |
∴PC=
| PO2+CO2 |
| 10 |
易知底面ABCD为矩形,从而OC=OD,PC=PD.
在△PCD中,cosPCD=
| ||
| PC |
| ||
| 10 |
∴异面直线AB和PC所成角的大小为arccos
| ||
| 10 |


练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 中,
中, ,
, 分别是
分别是 的中点,且
的中点,且
 .
.
 与
与 所成角的大小;
所成角的大小; 与平面
与平面 所成角的正弦值.
所成角的正弦值.  的底面为等腰直角三角形,
的底面为等腰直角三角形, ,
, ,
, 分别是
分别是 的中点。求异面直线
的中点。求异面直线 和
和 所成角的大小。
所成角的大小。