题目内容
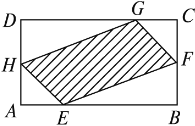
【题目】如图,有一块矩形空地,要在这块空地上开辟一个内接四边形为绿地,使其四个顶点分别落在矩形的四条边上,已知AB=a(a>2),BC=2,且AE=AH=CF=CG,设AE=x,绿地面积为y.
(1)写出y关于x的函数关系式,并指出这个函数的定义域;
(2)当AE为何值时,绿地面积y最大?
【答案】(1) y=-2x2+(a+2)x(0<x≤2);(2)详见解析.
【解析】
试题分析:(1)可以用减法,整个矩形的面积-4个直角三角形的面积得到阴影面积,根据矩形边长求函数定义域,、;(2)函数配方后可得
![]() ,讨论对称轴
,讨论对称轴![]() 和定义域端点值2的关系,定义域若包含对称轴,那顶点最大,若定义域不包含对称轴,那离对称轴近函数值大,分情况得到函数的最大值.
和定义域端点值2的关系,定义域若包含对称轴,那顶点最大,若定义域不包含对称轴,那离对称轴近函数值大,分情况得到函数的最大值.
试题解析:(1)由题意可知,S△AEH=S△CGF=![]() ,S△DHG=S△BEF=
,S△DHG=S△BEF=![]() (a-x)(2-x),
(a-x)(2-x),
所以y=![]() -2S△AEH-2S△BEF=2a-x2-(a-x)(2-x)=-2x2+(a+2)x.
-2S△AEH-2S△BEF=2a-x2-(a-x)(2-x)=-2x2+(a+2)x.
故函数解析式为y=-2x2+(a+2)x(0<x≤2).
(2)因为y=-2x2+(a+2)x (0<x≤2),
(0<x≤2),
当![]() ,即a<6时,则
,即a<6时,则![]() 时,y取最大值
时,y取最大值![]() ,
,
当![]() ,即a≥6时,y=-2x2+(a+2)x在x∈(0,2]上是增函数,
,即a≥6时,y=-2x2+(a+2)x在x∈(0,2]上是增函数,
则x=2时,y取最大值2a-4.
综上所述:当a<6时,AE=![]() 时,绿地面积取最大值
时,绿地面积取最大值![]() ;
;
当a≥6时,AE=2时,绿地面积取最大值2a-4.

练习册系列答案
相关题目
【题目】以下是某地搜集到的新房屋的销售价格y和房屋的面积x的数据:
房屋面积x(m2) | 115 | 110 | 80 | 135 | 105 |
销售价格y(万元) | 24.8 | 21.6 | 18.4 | 29.2 | 22 |
(1)画出数据对应的散点图;
(2)求线性回归方程,并在散点图中加上回归直线.
(参考公式![]() =
= ,
,![]() =
=![]()
![]() +
+![]() ,其中
,其中![]() =60 975,
=60 975,![]() =12 952)
=12 952)

