Question

【题目】已知定义在R上的函数是奇函数，函数的定义域为．

（1）求的值；

（2）若在上递减，根据单调性的定义求实数的取值范围；

（3）在（2）的条件下，若函数在区间上有且仅有两个不同的零点，求实数的取值范围．

Answer 1

【答案】（1）；（2）；（3）.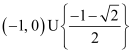

【解析】

试题分析：（1）因为函数是R上的奇函数，所以，求得；（2）根据定义法，设 时，需满足，这样可求得实数的取值范围；（3）将函数零点转化为的实根，是方程的一个实根，所以需讨论的实根情况，得到的取值范围.

试题解析：（1） 函数是奇函数

∴ ．

∴ 得．………………3分

（2）∵在上递减

∴ 任给实数 ，当 时

∴

∴ ………………………………………………6分

（3）由（1）得，令，即．

化简得． 或 ．

若是方程的根，则，

此时方程的另一根为1，与在区间上有且仅有两个不同的零点不符．

函数在区间上有且仅有两个不同的零点等价于方程

（※）在区间上有且仅有一个非零的实根．

①当时，得．

若，则方程（※）的根为，符合题意;

若，则与（2）条件下矛盾，不符合题意．

．

② 当时，令

由 得．

综上所述，所求实数的取值范围是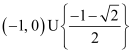． ………………12分