题目内容
(本小题满分13分)已知定义域为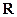 的函数
的函数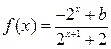 是奇函数.
是奇函数.
(1)求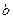 的值;(2)判断函数
的值;(2)判断函数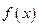 的单调性;
的单调性;
(3)若对任意的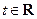 ,不等式恒成立
,不等式恒成立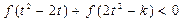 ,求k的取值范围.
,求k的取值范围.
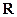 的函数
的函数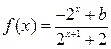 是奇函数.
是奇函数.(1)求
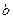 的值;(2)判断函数
的值;(2)判断函数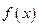 的单调性;
的单调性;(3)若对任意的
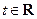 ,不等式恒成立
,不等式恒成立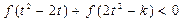 ,求k的取值范围.
,求k的取值范围.解:(1)因为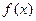 是奇函数,所以
是奇函数,所以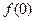 =0,
=0,
即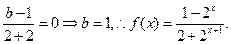 ………………………3
………………………3
(2)由(1)知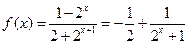 ,………………………5
,………………………5
设

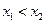 ,则
,则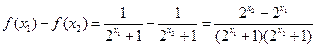 .
.
因为函数y=2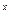 在R上是增函数且
在R上是增函数且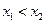 , ∴
, ∴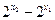 >0.
>0.
又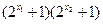 >0 ,∴
>0 ,∴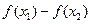 >0,即
>0,即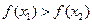 ,
,
∴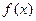 在
在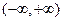 上为减函数.另法:或证明f′(x)
上为减函数.另法:或证明f′(x)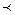 0………………………9
0………………………9
(3)因为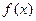 是奇函数,从而不等式
是奇函数,从而不等式
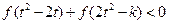 等价于
等价于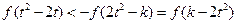 ,………………………3
,………………………3
因为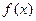 为减函数,由上式推得
为减函数,由上式推得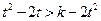 .即对一切
.即对一切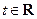 有
有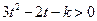 ,
,
从而判别式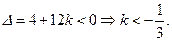 ………………………13
………………………13
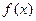 是奇函数,所以
是奇函数,所以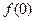 =0,
=0,即
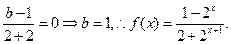 ………………………3
………………………3(2)由(1)知
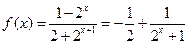 ,………………………5
,………………………5设


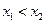 ,则
,则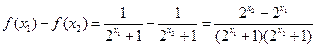 .
.因为函数y=2
 在R上是增函数且
在R上是增函数且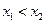 , ∴
, ∴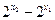 >0.
>0.又
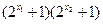 >0 ,∴
>0 ,∴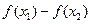 >0,即
>0,即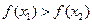 ,
,∴
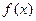 在
在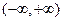 上为减函数.另法:或证明f′(x)
上为减函数.另法:或证明f′(x)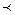 0………………………9
0………………………9(3)因为
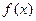 是奇函数,从而不等式
是奇函数,从而不等式 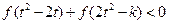 等价于
等价于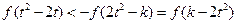 ,………………………3
,………………………3因为
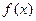 为减函数,由上式推得
为减函数,由上式推得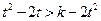 .即对一切
.即对一切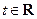 有
有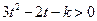 ,
, 从而判别式
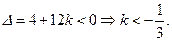 ………………………13
………………………13略

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
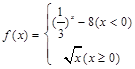 ,若f(a)>1,则实数a的取值范围是( )
,若f(a)>1,则实数a的取值范围是( )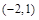
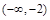 ∪
∪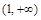
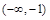 ∪(0,+∞)
∪(0,+∞)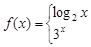
 ,则
,则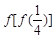 的值是( )
的值是( )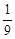

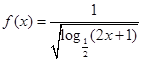 ,则
,则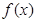 的定义域为( )
的定义域为( )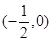
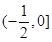
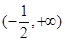
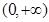
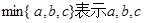 三个数中的最小值,设
三个数中的最小值,设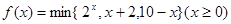 ,则
,则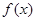 的最大值为 ( )
的最大值为 ( ) 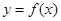 的定义域是
的定义域是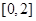 ,则函数
,则函数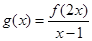 的定义域是( )
的定义域是( )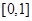


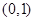
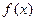 是
是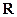 上的奇函数,且单调递减,解关于
上的奇函数,且单调递减,解关于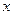 的不等式
的不等式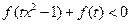 ,其中
,其中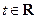 且
且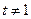 .
.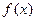 ,
,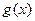 分别由下表给出
分别由下表给出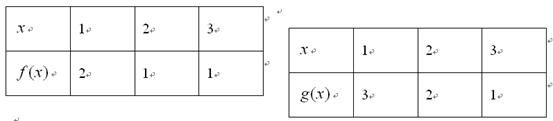
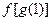 的值为 ;当
的值为 ;当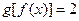 时,
时, .
.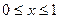 时,函数
时,函数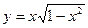 的最大值为
的最大值为