题目内容
圆C1:(x-2)2+(y+2)2=9与圆C2:(x+1)2+(y-2)2=4的公切线有( )
| A.0条 | B.2条 | C.3条 | D.4条 |
C
解析试题分析:两个圆的圆心距为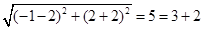 ,即两个圆的圆心距等于两个圆的半径的和,所以两个圆相外切,所以两个圆的公切线有3条.
,即两个圆的圆心距等于两个圆的半径的和,所以两个圆相外切,所以两个圆的公切线有3条.
考点:本小题主要考查两个圆的位置关系和公切线的条数.
点评:判断两个圆的位置关系,主要是看两个圆的圆心距和半径的和与查之间的关系.

练习册系列答案
相关题目
若方程 的任意一组解
的任意一组解 都满足不等式
都满足不等式 ,则
,则 的取值范围是
的取值范围是
A. | B. | C. | D.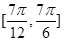 |
若过定点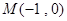 且斜率为
且斜率为 的直线与圆
的直线与圆 在第一象限内的部分有交点,则
在第一象限内的部分有交点,则 的取值范围是( ).
的取值范围是( ).
A. | B.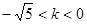 |
C. | D. |
已知圆 :
: ,过
,过 轴上的点
轴上的点 存在圆
存在圆 的割线
的割线 ,使得
,使得 ,则点
,则点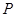 的横坐标
的横坐标 的取值范围是( )
的取值范围是( )
A. | B. | C. | D. |
若直线 截得的弦最短,则直线
截得的弦最短,则直线 的方程是
的方程是
A. | B. |
C. | D. |
若直线 与圆
与圆 有公共点,则实数
有公共点,则实数 取值范围是( )
取值范围是( )
A. | B. |
C. | D. |
圆 :
: 与圆
与圆 :
: 的位置关系是( )
的位置关系是( )
| A.相交 | B.外切 | C.内切 | D.相离 |
以两点 和
和 为直径端点的圆的方程是
为直径端点的圆的方程是
A. | B. |
C. | D. |
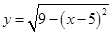 的图象上存在不同的三点到原点的距离构成等比数列,则以下不可能成为该等比数列的公比的数是( )
的图象上存在不同的三点到原点的距离构成等比数列,则以下不可能成为该等比数列的公比的数是( )


