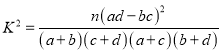题目内容
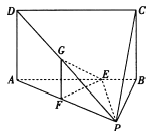
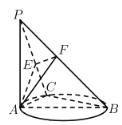
【题目】如图所示, ![]() 平面
平面![]() ,点
,点![]() 在以
在以![]() 为直径的
为直径的![]() 上,
上, ![]() ,
, ![]() ,点
,点![]() 为线段
为线段![]() 的中点,点
的中点,点![]() 在
在![]() 上,且
上,且![]() .
.
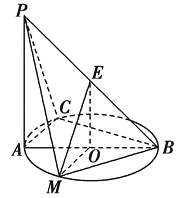
(Ⅰ)求证: 平面![]() 平面
平面![]() ;
;
(Ⅱ)求证: 平面![]() 平面
平面![]() .
.
【答案】(Ⅰ)证明见解析;(Ⅱ)证明见解析.
【解析】试题分析:(Ⅰ)利用三角形的中位线定理可得![]() ,即可得出
,即可得出![]() 平面
平面![]() ,再利用
,再利用![]() ,可得
,可得![]() 平面
平面![]() ,再利用面面平行的判定定理即可得出平面
,再利用面面平行的判定定理即可得出平面![]() 平面
平面![]() ;(Ⅱ)点
;(Ⅱ)点![]() 在以
在以![]() 为直径的
为直径的![]() 上,可得
上,可得![]() ,利用
,利用![]() 平面
平面![]() ,可得
,可得![]() ,可得
,可得![]() 平面
平面![]() ,即可得出平面
,即可得出平面![]() 平面
平面![]() .
.
试题解析:证明:(Ⅰ)因为点![]() 为线段
为线段![]() 的中点,点
的中点,点![]() 为线段
为线段![]() 的中点,所以
的中点,所以![]() .
.
因为![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .因为
.因为![]() ,
,
又![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.
因为![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
, ![]() ,
,
所以平面![]() 平面
平面![]() .
.
(2)因为点![]() 在以
在以![]() 为直径的
为直径的![]() 上,所以
上,所以![]() ,即
,即![]() .
.
因为![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,所以
,所以![]() . 因为
. 因为![]() 平面
平面![]() ,
, ![]() 平面,
平面, ![]() ,所以
,所以![]() 平面
平面![]() .
.
因为![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]()

练习册系列答案
相关题目
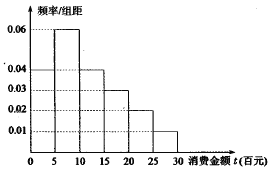
【题目】某单位鼓励员工参加健身运动,推广了一款手机软件,记录每人每天走路消耗的卡路里;软件的测评人员从员工中随机地选取了40人(男女各20人),记录他们某一天消耗的卡路里,并将数据整理如下:
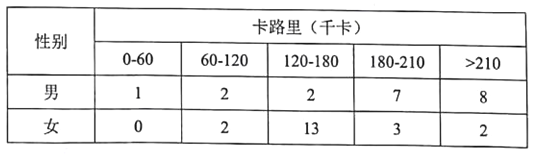
(1)已知某人一天的走路消耗卡路里超过180千卡被评测为“积极型”,否则为“懈怠型”,根据题中数据完成下面的![]() 列联表,并据此判断能否有99%以上把握认为“评定类型”与“性别”有关?
列联表,并据此判断能否有99%以上把握认为“评定类型”与“性别”有关?
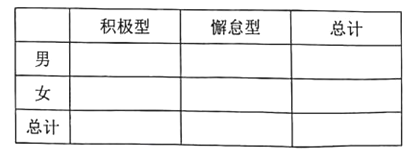
(2)若测评人员以这40位员工每日走路所消耗的卡路里的频率分布来估计其所有员工每日走路消耗卡路里的频率分布,现在测评人员从所有员工中任选2人,其中每日走路消耗卡路里不超过120千卡的有![]() 人,超过210千卡的有
人,超过210千卡的有![]() 人,设
人,设![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
附: 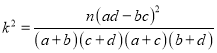 ,其中
,其中![]() .
.
参考数据:
| 0.10 | 0.05 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |